电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] .
目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递.
此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差.
针对上述问题,本文建立BESSs双层多目标优化配置模型,并设计性能良好的优化算法求解BESSs优化配置方案:
(1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好.
(2) 对BESSs优化配置模型进行双层架构,将建立的多目标优化模型作为外层模型,以求解BESSs选址定容方案;内层模型则以最大化BESSs运营效益为目标求解其充放电运行策略.相较于单层优化和上下层独立循环的双层优化[11 ] ,所构建的双层模型考虑了BESSs规划和运行之间的联系,通过内外层的嵌套循环迭代,保证了优化配置方案的有效性.
(3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷.
(4) 采用聚类算法对全年的负荷曲线和风、光出力曲线进行典型日聚类,基于其时序特性组合得到4种典型场景.在不同典型场景下分别进行仿真计算,得到各目标函数的全年总和,更好地反映了负荷和新能源在全年的不确定性.以扩展的IEEE-33节点配电系统为例进行仿真测试,验证了所提方法的有效性.
1 BESSs双层多目标优化配置模型
鉴于BESSs的后期运行与初期规划相互影响,并考虑BESSs选址定容方案与其充放电功率之间的耦合关系,建立BESSs双层多目标优化配置模型.一方面,将长时间尺度的BESSs规划问题放在外层模型,短时间尺度的BESSs运行问题放在内层模型,通过内外层优化的有效衔接,使得BESSs规划方案更合理,且更符合实际运行,有助于提高BESSs的利用率.另一方面,将BESSs充放电功率放于内层进行优化,使得外层模型的决策变量维度呈指数式缩减,可有效提高Pareto解集的分布性,并加快收敛速度.
1.1 BESSs最优选址定容规划
外层以BESSs年投资运维成本、配电网年电压波动和年负荷波动最小为目标,建立考虑BESSs投资成本效益和配电网运行可靠性的Pareto多目标优化模型:
(1) m i n X F h ( X , x ) , h = 1,2 , 3 s . t . g ( X , x ) ≤ 0
式中:$F_{h}(\boldsymbol{X},\boldsymbol{x})$为外层模型的第h个目标函数;X和x分别为外层和内层模型的决策变量向量;$g(\boldsymbol{X}, \boldsymbol{x})$为外层模型需满足的约束条件.
1.1.1 目标函数
BESSs的年投资运维成本.投资方往往以成本效益为原则配置BESSs,投资效益主要来自于BESSs的低储高发套利.BESSs年投资运维成本为
1.1.1 目标函数
BESSs的年投资运维成本.投资方往往以成本效益为原则配置BESSs,投资效益主要来自于BESSs的低储高发套利.BESSs年投资运维成本为
(2) F 1 = C T C C + C O M - I S - P - I s u b
式中:C TCC 和C OM 分别为BESSs的等年值投资成本和年运行维护成本;I S-P 和I sub 分别为每年的低储高发套利和发售电量的政府补贴.
(3) C T C C = [ C i n v N B E S S + ∑ n = 1 N B E S S ( a P B E S S , n + b E B E S S , n ) ] μ C R F μ C R F = r ( 1 + r ) y ( 1 + r ) y - 1
式中:C inv 为单台BESS的固定投资成本;N BESS 为BESSs的安装数量;E BESS, n P BESS, n n 台BESSs的配置容量和功率;a 和b 分别为BESSs的单位功率成本和不同充电倍率(C rate )下的单位容量成本;μ CRF 为年资金回收率;y 为BESSs的使用年限,本文取y =10;r 为折现率,采用加权平均资金成本[18 ] 计算.需说明的是,在目标函数计算中,把一年分为多个典型场景计算,同时考虑BESSs的投资运行年限,将所有资金折算成现值.
(4) C O M = ρ o m ∑ n = 1 N B E S S ( a P B E S S , n + b E B E S S , n )
式中:ρ om 为运维系数,即BESSs年运维费用占设备投资成本的比率,约为1%~10%[19 ] .
(5) I S - P = ∑ m - 1 M d D m ∑ n = 1 N B E S S ∑ t = 1 T ( ρ s e l l ( t ) P d i s , n ( t ) - ρ p u r ( t ) P c h a , n ( t ) )
式中:M d D m m ρ p u r ( t ) ρ s e l l ( t )
t [20 ] ;P c h a , n ( t ) P d i s , n ( t ) n t 时段内的充电和放电功率;T =24 h.
(6) I s u b = ∑ m = 1 M d D m ∑ n = 1 N B E S S ∑ t = 1 T ( λ P d i s , n ( t ) )
配电网的年电压波动.BESSs可通过功率控制减小节点电压波动.在BESSs的选址定容规划中考虑配电网的电压质量,用全年的电压波动总和表示:
(7) F 2 = ∑ m = 1 M d D m ∑ j = 1 N n o d e s ∑ t = 1 T V j ( t ) - V - j
式中:N nodes 为系统节点总数;V j ( t ) j t V - j j
配电网的年负荷波动.BESSs具有快速能量吞吐能力,可对负荷波动进行平抑.在BESSs的选址定容规划中同时考虑了配电网的功率稳定性,用全年的负荷标准差之和表示:
(8) F 3 = ∑ m = 1 M d D m ∑ t = 1 T [ ( P l o a d ( t ) - P P V ( t ) - P w i n d ( t ) - P c h a / d i s ( t ) - P - L ) 2 / T ]
式中: P l o a d ( t ) P P V ( t ) ( t)和P w i n d ( t ) t P c h a / d i s ( t ) t 时段的充放电功率;P - L
P - L = ∑ t = 1 T ( P l o a d ( t ) - P P V ( t ) - P w i n d ( t ) - P c h a / d i s ( t ) ) T
1.1.2 约束条件
外层模型的约束条件主要包括两类:一类是系统运行约束,即节点功率平衡约束、节点电压约束、并网点功率约束、弃风弃光约束,该类约束以网络潮流的计算结果为依据,以确保整个配电网运行状态的安全性和可靠性,并通过满足弃风弃光率来尽可能促进新能源的就地消纳;另一类是BESSs配置约束,即安装位置约束、功率和容量约束,以满足外层决策变量范围的限制约束.
(9) P i ( t ) - ( G i j c o s θ i j ( t ) + B i j s i n θ i j ( t ) ) V i ( t ) ∑ j = 1 N n o d e s V j ( t ) = 0 Q i ( t ) - ( G i j s i n θ i j ( t ) - B i j c o s θ i j ( t ) ) V i ( t ) ∑ j = 1 N n o d e s V j ( t ) = 0
式中: P i ( t ) Q i ( t ) t i V i ( t ) V j ( t ) t i j θ i j ( t ) t i j G i j B i j i j
(10) V i m i n ≤ V i ( t ) ≤ V i m a x
V i m a x V i m i n i
(11) V i ( t ) = { [ V j ( t ) - ( r i j P i j ( t ) + x i j Q i j ( t ) ) ] 2 + ( r i j P i j ( t ) + x i j Q i j ( t ) ) 2 } 1 2
式中:P i j ( t ) Q i j ( t ) i j r i j x i j i j
(12) P g r i d m i n ≤ P g r i d ( t ) ≤ P g r i d m a x Q g r i d m i n ≤ Q g r i d ( t ) ≤ Q g r i d m a x
式中:P g r i d ( t ) Q g r i d ( t ) P g r i d m a x P g r i d m i n Q g r i d m a x Q g r i d m i n
(13) R c u r ≤ R c u r , m a x
式中:R cur,max 为最大年弃风弃光率,设为5%[21 ] ;R cur 为年弃风弃光率,且
(14) R c u r = ∑ m = 1 M d D m ∑ t = 1 T ( P P V ( t ) + P w i n d ( t ) + P c h a / d i s ( t ) - P l o a d ( t ) - P l o s s ( t ) ) / [ ∑ m = 1 M d D m ∑ t = 1 T ( P P V ( t ) + P w i n d ( t ) ) ]
(15) L B E S S , n ∈ N n o d e s 且 L B E S S , n ≠ L g r i d L B E S S , n ≠ L B E S S , n + 1
式中:L BESS, n L grid 为配网与主网的联络点.需说明的是,BESSs可以安装在除联络点以外的任一节点,但不能安装在同一个节点.
(16) E B E S S m i n ≤ E B E S S , n ≤ E B E S S m a x P B E S S m i n ≤ P B E S S , n ≤ P B E S S m a x
式中:E B E S S m a x E B E S S m i n P B E S S m a x P B E S S m i n
1.2 BESSs最优充放电运行
内层模型以BESSs年运营收益最大为目标,建立BESSs充放电运行优化模型:
(17) m a x x f ( X , x ) s . t . g ' ( X , x ) ≤ 0
式中:f ( X , x ) 为 内 层 模 型 的 目 标 函 数 ; g ' ( X , x )
1.2.1 目标函数
在外层规划保证了配电网可靠运行的前提下,BESSs运营方旨在最大化年运营效益,主要包括低储高发套利、降损效益和环境效益.BESSs年运营效益定义为
(18) f = I S - P + I s u b + Δ I P l o s s + Δ I E N V
式中:ΔI Ploss 和ΔI ENV 分别为配置BESSs后每年的降损效益和环境效益.
(19) Δ I P l o s s = ∑ m = 1 M d D m ∑ t = 1 T ( ρ s e l l ( t ) | Δ P l o s s ( t ) | )
式中:Δ P l o s s ( t ) t 时段内减少的功率损耗.
(20) Δ I E N V = ∑ m = 1 M d D m ∑ t = 1 T Δ P g r i d ( t ) ∑ p = 1 P ( U p u p ) s . t . P g r i d ( t ) > 0
式中:Δ P g r i d ( t ) P U p p u p p [22 ] .
1.2.2 约束条件
内层模型的约束条件除系统运行约束和BESSs配置约束以外,还设置了BESSs充放电约束、荷电状态(State of Charge, SOC)约束和BESSs充电倍率约束,旨在降低BESSs的寿命损耗和运行成本.
(21) 0 ≤ P c h a , n ( t ) ≤ P B E S S , n η c h a - P B E S S , n / η d i s ≤ P d i s , n ( t ) ≤ 0
式中:η cha 和η dis 分别为BESSs的充电效率和放电效率.
(22) S O C m i n ≤ S O C n ( t ) ≤ S O C m a x
式中:SOCmin =20%、SOCmax =90%;SOCn t 时段的SOC,有
(23) S O C n ( t ) = ( 1 - δ Δ t ) S O C n ( t - 1 ) + P c h a , n ( t ) Δ t η c h a , 充 电 S O C n ( t ) = ( 1 - δ Δ t ) S O C n ( t - 1 ) - P d i s , n ( t ) Δ t / η d i s , 放 电
式中:δ 为BESSs的自放电率;Δt 为BESSs的充放电时长.
(24) C r a t e ≤ 4 C C r a t e = k ' C , k ' = 0.5,1 , 2,4
式中:C 为BESSs在1 h内完全放电时的电流强度.
2 求解方案设计
2.1 基于孔雀优化算法的内层模型求解
在模型内层,采用寻优性能良好的POA求解最优的BESSs充放电运行策略,并在算法内部调用Matpower工具箱采用快速解耦算法进行配电网潮流计算.POA的算法原理和验证参见文献[23 ],本文仅对算法的寻优机制进行简述.
2.1.1 孔雀优化算法
POA通过雄孔雀求偶、雌孔雀自适应接近雄孔雀、幼孔雀自适应搜索食物源和雄孔雀交互4种寻优机制完成迭代更新,以逐渐逼近问题最优解.过程中,所有孔雀根据其适应度值的排序进行角色分配,具有最高适合度值的前5只为雄孔雀,剩下的前30%为雌孔雀,其余为幼孔雀.
(25) x c , 1 = x c , 1 ( t ) + R s x r , 1 ‖ x r , 1 ‖ x c , n = x c , N ( t ) + σ R s x r , N ‖ x r , N ‖ , 若 r N < ε x c , N ( t ) , 否 则
式中:x c , 1 x c , N N = 2 , 3 , 4 , 5 ; σ ε N = 2 , 3 , 4 , 5 σ = 1.5 , 2 , 3 , 5 ε = 0.9 , 0.8 , 0.6 , 0.3 r N x r , 1 x r , N
(26) x r = 2 r a n d ( 1 , D i m ) - 1
(27) R s ( t ) = R s 0 - ( R s 0 - 0 ) ( k / k m a x ) 0.01 R s 0 = C v ( x u b - x l b )
式中:Dim为决策变量的数量;0表示孔雀绕圈旋转的圆心;k 和k max 分别为当前迭代次数和最大迭代次数;R s0 为初始旋转半径;C v 为雄孔雀旋转因子,设为0.2;x ub 和x lb 为决策变量的上下限.
在该机制下,适应度值越高的雄孔雀围绕食物源旋转的概率越大,且绕圈半径越小,因此更趋近于局部最优解.可见,雄孔雀位置代表的决策变量解趋近最优解的能力与其适应度值成正相关,与绕圈半径成负相关.
(28) $\boldsymbol{x}_{\mathrm{h}}=\boldsymbol{x}_{\mathrm{h}}(t)+3 \theta\left(\boldsymbol{x}_{\mathrm{c}, N}-\boldsymbol{x}_{\mathrm{h}}(t)\right), \quad \text { 若 } r_{5} \in A$
式中:x h r 5 A N = 1,2 , 3,4 , 5 [ 0.6,1 ) [ 0.4,0.6 ) [ 0.2,0.4 ) [ 0.1,0.2 ) [ 0,0.1 ) θ
(29) θ = θ 0 + ( θ 1 - θ 0 ) k / k m a x
在该机制下,当θ<1/3时(迭代初期),雌孔雀趋向于所选择的雄孔雀,进行局部勘测;当θ>1/3时(迭代中后期),雌孔雀倾于向所选雄孔雀相对的位置移动,进行全局搜索.因此,较小的θ θ
幼孔雀自适应搜索食物源.幼孔雀向雄孔雀移动的同时借助Levy飞行机制[24 ] 在搜索空间进行随机搜索:
(30) x c u = x c u ( t ) + α L e v y ( x c , 1 ( t ) - x c u ( t ) ) + β ( x p u ( t ) - x c u ( t ) ) x p u = x c , N ( t ) , r 6 ∈ B
式中:x c u x p u r 6 α α
(31) α = α 0 ( α 0 - α 1 ) ( k / k m a x ) 2 β = β 0 + ( β 1 - β 0 ) ( k / k m a x ) 0.5
式中:α 0 = 0.9 α 1 = 0.4 、 β 0 = 0.1 、 β 1 = 1 .
在该机制下,当α > β β > α α β
雄孔雀交互行为.拥有最佳食物源的第1只雄孔雀被视为领导者,第2~4只雄孔雀逐渐向第1只雄孔雀移动:
(32) x c , N = x c , N ( t ) + θ d N + r ' N D N ‖ D N ‖
d N = x c , 1 - x c , N D N = x ' r , N - x ' r , N d N d N d N d N
r ' n x ' r , N
2.1.2 BESSs充放电校验
内层优化实际上是一个时序耦合优化问题,即BESSs的运行约束与多个时段关联.在常规网络潮流的基础上进行多时段的扩展,以保证BESSs在各时段的充放电运行均最优,即采用POA求解BESSs在24个时段的充放电功率,基于Matpower工具箱对每个时段单独进行潮流计算.另外,鉴于BESSs在充放电过程中可能会出现超出SOC安全裕度的情况,导致BESSs容量空间未被充分利用或是超出安全运行范围.因此,设置SOC安全约束,对BESSs的充放电功率进行校验和修正:
(33) P c h a , n ( t ) = m i n { P B E S S m a x , [ ( 1 - δ ) E n ( t ) - S O C m i n E B E S S , n ] / η c h a } , s . t . E n ( t + 1 ) < S O C m i n E B E S S , n P c h a , n ( t ) = m i n { P B E S S m a x , [ ( 1 - δ ) E n ( t ) - S O C m a x E B E S S , n ] / η c h a } , s . t . E n ( t + 1 ) > S O C m a x E B E S S , n E n ( t + 1 ) = ( 1 - δ ) E n ( t ) - η c h a P c h a , n ( t )
(34) P d i s , n ( t ) = m i n { - P B E S S m a x , [ ( 1 - δ ) E n ( t ) - S O C m i n E B E S S , n ] η d i s } , s . t . E n ( t + 1 ) < S O C m i n E B E S S , n P d i s , n ( t ) = m i n { - P B E S S m a x , [ ( 1 - δ ) E n ( t ) - S O C m a x E B E S S , n ] η d i s } , s . t . E n ( t + 1 ) > S O C m a x E B E S S , n E n ( t + 1 ) = ( 1 - δ ) E n ( t ) - P c h a , n ( t ) / η d i s
式中E n ( t + 1 ) E n ( t ) B E S S s t + 1 t
2.2 基于多目标孔雀优化算法的外层模型求解
在模型外层,设计基于Pareto的MOPOA求解BESSs的最佳选址定容方案.首先,根据式(25)~(32)逐代更新外层孔雀种群的位置,以不断更新BESSs选址定容方案的Pareto解集.进而,采用改进理想点决策(Improved Ideal Point Based Decision, IIPBD)[25 ] 方法决策BESSs最佳选址定容方案.
2.2.1 Pareto解集存储与筛选
在算法迭代过程中,采用外部归档集来存储Pareto非支配解集.MOPOA-POA在每次迭代中获得的新非支配解集,须逐一与原非支配解集进行比较并更新外部归档集[26 ] :① 若新解支配归档集里的某一个或多个解,则将归档集中被支配的解替换为新解;② 若归档集里至少有一个解支配新解,则放弃新解;③ 若新解与归档集里的所有解均互不支配,则将新解放入外部归档集.
为增加解的多样性,当归档集中非支配解的数量超过上限时,需剔除多余的解.采用拥挤距离排序法选出分布较密集的一组非支配解集,并通过轮盘赌法剔除多余解集.非支配解的相邻解数量越多,被剔除的概率就越大.
2.2.2 改进理想点决策 首先,对所有Pareto非支配解的适应度值进行归一化处理:
(35) y h ( χ i ) = F h ( x i ) - F h m i n F h m a x - F h m i n , h = 1 , 2 , 3
式中: y h ( χ i ) i h F h P a r e t o F h m a x F h m i n
其次,计算各个非支配解到目标理想点的趋近度,即欧氏距离平方:
(36) E U ( χ i ) = ∑ h = 1 3 ( y h ( χ i ) - 0 ) 2 ω h 2
最后,以所有Pareto非支配解在各个目标上的欧氏距离平方之和最小为原则来客观地确定BESSs选址定容的最佳折中决策方案:
(37) $\chi_{\text {best }}=\arg \min _{i=1,2, \cdots, n_{\mathrm{r} h=1}}^{3}\left(y_{h}\left(\chi_{i}\right)-0\right)^{2} \omega h^{2}$
式中:n r 为外部归档集中Pareto非支配解的数量.
2.3 算法应用设计
构建的BESSs双层多目标优化配置模型是一个含多维变量、多个目标、多项约束的高度非线性复杂优化模型,分别应用POA和MOPOA对内层和外层模型进行求解,在算法内部调用Matpower工具箱进行基于快速解耦算法的配电网潮流计算.
(1) 决策变量设置.内层优化的决策变量为由BESSs分别在24个时段的充放电运行功率构成的优化向量,即为POA算法中每只孔雀的位置向量,所有孔雀随迭代过程不断进行位置更新.BESSs外层优化的决策变量包括BESSs的安装位置、配置功率和容量.特别地,BESSs安装位置为离散变量,通过在连续空间取整即可.其中,外层所得BESSs配置功率即为内层BESSs充放电功率的上下限,即式(21);BESSs配置功率和配置容量在设定变量范围内还应满足充电倍率约束,即式(24).
(2) 适应度函数处理.算法的适应度函数须有效结合BESSs优化配置模型的目标和约束条件.其中,不等式约束采用罚函数的形式将其加到原目标函数上进行处理.第h 个目标函数对应的算法适应度函数设计为
(38) F h ( x i ) = F h ( x i ) + η q
式中:η 为惩罚系数,取正无穷;q 为违背约束条件的个数.
(3) 算法求解流程:① 根据配电网参数和时序运行数据,初始化外层孔雀群的位置和各适应度值,获得初始化的BESSs安装位置、容量和功率;② 将外层得到的BESSs选址定容方案输入内层模型,并初始化内层孔雀群的位置和适应度值;③ 在内层循环迭代过程中,采用POA对内层孔雀群的位置和适应度值进行更新,直到内层最大迭代次数,则输出内层最优解,即BESSs在24个时段的充放电功率;④ 将内层迭代得到的BESSs最优充放电运行策略输入外层模型,计算外层孔雀群的各适应度值;⑤ 在外层循环迭代过程中,采用MOPOA更新外层孔雀群的位置和外部归档集,并筛选Pareto非支配解集;⑥重复步骤④~⑤,直到外层最大迭代次数,则输出一组完整且均匀分布的外层Pareto非支配解集;⑦利用IIPBD从外层Pareto非支配解集中挑选BESSs选址定容的最佳折中决策方案,即最优的BESSs安装位置、容量和功率;⑧将BESSs最优选址定容方案输入内层模型,重复步骤③~⑦.
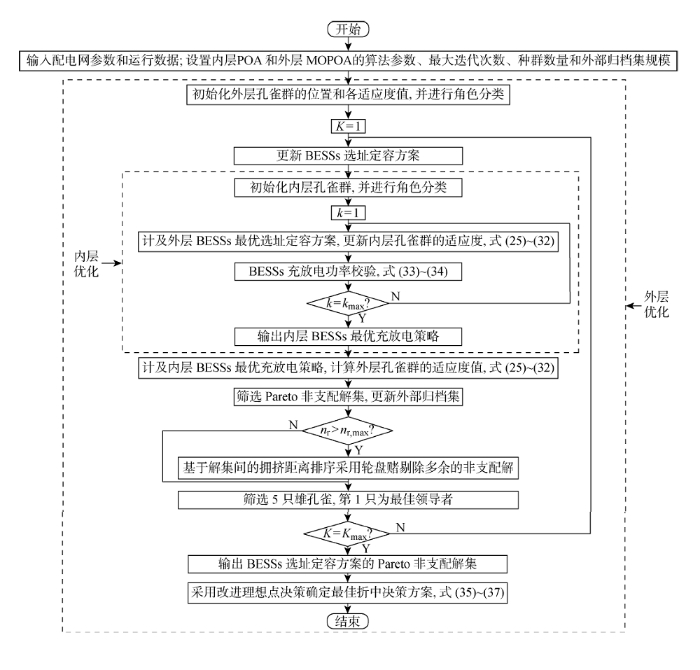
综上,所提BESSs双层多目标优化配置的具体流程如图1 所示.其中,K 为外层优化的迭代次数.
图1
图1
BESSs双层多目标优化配置的流程图
Fig.1
Flow chart of bi-level multi-objective optimal allocation of BESSs
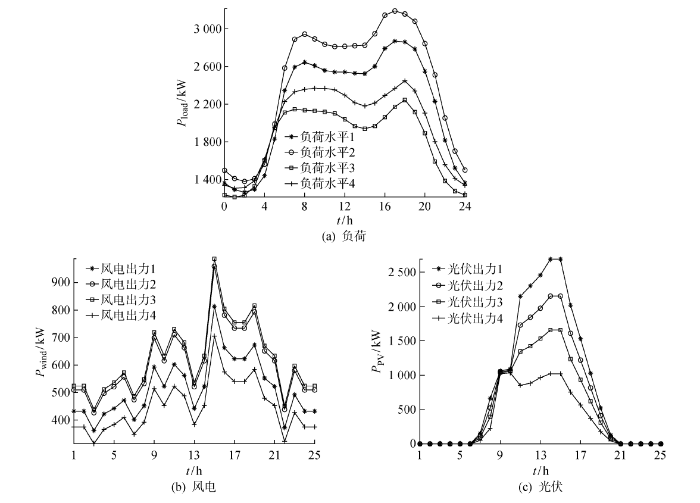
3 运行场景聚类
考虑负荷、风电和光伏出力的不确定性,采用多个典型日场景下的负荷、风电和光伏出力曲线代表全年,更好地反映负荷和新能源在全年的不确定性.首先,采用一种模糊核C -均值聚类算法[27 ] 处理云南省某地的年历史数据,分别得到负荷、风电和光伏的典型日曲线,如图2 所示.进而,综合考虑负3种曲线的相关性,通过场景组合得到4种典型场景,每种场景的组合方式及对应天数如表1 所示.
图2
图2
负荷、风电和光伏的典型日曲线
Fig.2
Typical diurnal curves of load, wind, and PV power
4 算例分析
4.1 仿真模型
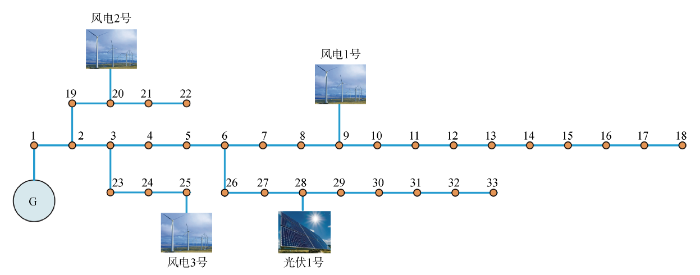
采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算.
图3
图3
扩展的IEEE-33节点系统拓扑图
Fig.3
Topology of extended IEEE-33 bus system
4.2 算法性能比较
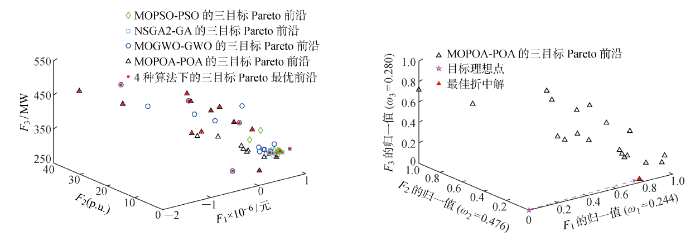
图4 和图5 (a)分别为4种算法在IEEE-33节点系统获得的两目标和三目标Pareto前沿.需说明的是,不同算法的Pareto前沿由其Pareto非支配解集中的解构成.从图中可知,在同样的迭代次数、种群数量及外部归档集规模条件下,MOPOA-POA获得的两目标和三目标Pareto前沿明显比其他3种算法延伸范围更广、分布更均匀.另外,将4种算法分别得到的Pareto非支配解集对应的目标值全部组合起来,确定该组合解集的Pareto前沿,以此作为所有算法求解该多目标优化问题的近似Pareto最优前沿[31 ] .比较不同算法的Pareto前沿与近似Pareto最优前沿的差距,可知由MOPOA-POA求得的Pareto前沿与该多目标优化问题的近似Pareto最优前沿重合度更高,因此本文所提算法的多目标优化性能较优.图5 (b)为采用IIPBD方法从
图4
图4
不同算法的两目标Pareto前沿
Fig.4
Bi-objective Pareto front obtained by different algorithms
图5
图5
三目标Pareto寻优结果
Fig.5
Results of three-objective Pareto front
MOPOA-POA获得的Pareto非支配解集中选取BESSs选址定容方案的最佳折中解.图中数值为各量的归一化值,ω 1 ω 2 ω 3 F 1 F 2 F 3 ω 1 + ω 2 + ω 3 = 1 .
表3 给为4种算法在外层模型获得的Pareto优化统计结果.可知,MOPOA-POA的Pareto解集在各个目标下的最好(小)值和最差(大)值的差均是最大的,进一步说明其Pareto解集分布广泛,算法的全局搜索能力最强;同时,在BESSs年投资运维成本和配电网年负荷波动两个目标下,MOPOA-POA的最好值是最小的,而配电网年电压波动仅次于MOGWO-GWO,可见算法的局部搜索能力也较强.因此,MOPOA-POA可以获得一组更合理的Pareto非支配解集,为决策者提供多个不同偏好的候选方案.
另外,采用世代距离(Generational Distance, GD)、反转世代距离(Inverted Generational distance, IGD)、空间分布(Spacing, SP)、广泛性、纯粹多样性(Pure Diversity, PD)、分布度指标(Diversity Metric, DM)、超体积(Hyper Volume, HV)定量评估算法的Pareto解集性能[32 ] ,结果如表4 所示.可知, MOPOA-POA的GD和IGD指标最低,
故收敛性能最佳;具有最小的SP和广泛性指标,故Pareto解集的分布最广泛且均匀;PD和DM指标最高,故分布度最高;而HV指标仅低于MOGWO-GWO,故多样性较好.综上, MOPOA-POA拥有优良的最优解搜索能力和Pareto解集寻优能力.
4.3 结果分析
表5 为基于IIPBD的MOPSO-PSO、NSGAII-GA、MOGWO-GWO、MOPOA-POA(算法1~4),以及基于加权求和(Weighted Sum, WS)的POA-POA(算法5)共5种算法获得的BESSs优化配置方案和双层优化结果.其中,为验证IIPBD的有效性,基于WS的POA-POA算法通过简化处理BESSs外层多目标优化模型,即主观地设定3个目标函数的权重均为1/3,从而将多目标问题转化为单目标问题.可知,相比其他算法,基于IIPBD的MOPOA-POA算法得到的BESSs配置方案具有最小的BESSs年投资运维成本和配电网年电压波动,而配电网年负荷波动值仅高于MOGWO-GWO,并且BESSs年运营收益最高.因此,MOPOA-POA算法在保证经济效益的同时可以给配电网带来最佳的综合优化效果,而且IIPBD可以获得更为客观的目标权重系数和折中解,避免采取主观权重而导致对某一目标产生较大偏好,从而获得了较合理的BESSs优化配置方案.
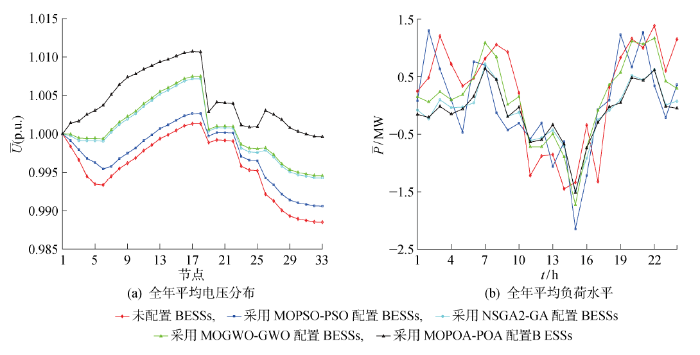
图6 为基于4种双层多目标优化算法配置BESSs后的IEEE-33节点配电网电压分布(U - ) 和负荷水平(P - ). 可知,与未配置BESSs相比,采用4种算法配置BESSs均能在一定程度上改善电压分布和负荷水平.特别地,算法4可显著提高配电网的节点电压分布,并改善配电网负荷波动情况.另外,算法1~4的BESSs优化配置方案均满足配电网弃风弃光约束,分别为3.27%、3.92%、3.64%、2.71%,相较于其他算法,算法4拥有最小弃风弃光率.综上,本文所提方法在解决配电网BESSs规划问题具有一定的有效性和优越性.
图6
图6
IEEE-33节点系统下4种算法的配电网优化结果
Fig.6
Optimization results of distribution network obtained by four algorithms in IEEE 33-bus system
由IEEE-33节点系统参数[26 ] 可知,节点6、7、23、24、29为系统重负荷节点,所提算法将2台BESSs分别配置在节点7和节点23,以满足重负荷地区的电能需要,并尽可能消纳新能源出力.特别地,安装在线路上游的BESS容量最大,可以更好地提升节点电压、降低网损.另外,所配置BESSs的充电倍率均为4C ,虽然增加了容量成本,但高充电倍率下电池的恒流充电时间更短,更能满足电网对BESSs的响应要求,也能较大发挥BESSs的充放电能力,从而获得较高的运营收益.然而,较高的充电倍率也会加速电池的容量衰减快慢,影响电池寿命,而本文未考虑BESSs的循环寿命损耗,乃不妥之处.
5 结语
本文设计了一种BESSs优化配置方法.首先,兼顾BESSs投资效益和配电网运行质量,建立BESSs双层多目标优化配置模型;其次,设计寻优性能良好的POA和MOPOA,分别对内层模型和外层模型进行可靠求解.通过内外层的嵌套循环迭代,最终形成综合考虑长期规划经济性和短期运行高效性的BESSs优化配置方案.IEEE-33节点系统的仿真结果显示,所提方法不仅可以实现BESSs投资经济性、配电网电压质量和功率稳定性的最佳权衡,而且可以实现BESSs年运营收益的最大化.
未来研究将提高算法收敛性能并增加算法的种群规模,同时考虑BESSs的循环寿命损耗,以提高配置的合理性.
参考文献
View Option
[1]
YANG B WANG J T CHEN Y X et al. Optimal sizing and placement of energy storage system in power grids: A state-of-the-art one-stop handbook
[J]. Journal of Energy Storage 2020 , 32 : 101814 .
[本文引用: 1]
[2]
YANG B YU L CHEN Y X et al. Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey
[J]. International Journal of Energy Research 2021 , 45 (3 ): 3615 -3642 .
DOI:10.1002/er.6104
URL
[本文引用: 1]
[3]
孙立明 , 杨博 . 蓄电池/超导混合储能系统非线性鲁棒分数阶控制
[J]. 电力系统保护与控制 2020 , 48 (22 ): 76 -83 .
[本文引用: 1]
SUN Liming YANG Bo Nonlinear robust fractional-order control of battery/SMES hybrid energy storage systems
[J]. Power System Protection and Control 2020 , 48 (22 ): 76 -83 .
[本文引用: 1]
[4]
YANG B WANG J B WANG J T et al. Robust fractional-order PID control of supercapacitor energy storage systems for distribution network applications: A perturbation compensation based approach
[J]. Journal of Cleaner Production 2021 , 279 : 123362 .
DOI:10.1016/j.jclepro.2020.123362
URL
[本文引用: 1]
[5]
YANG B WANG J T ZHANG X S et al. Control of SMES systems in distribution networks with renewable energy integration: A perturbation estimation approach
[J]. Energy 2020 , 202 : 117753 .
DOI:10.1016/j.energy.2020.117753
URL
[本文引用: 1]
[6]
YANG B WANG J B ZHANG X S et al. Applications of battery/supercapacitor hybrid energy storage systems for electric vehicles using perturbation observer based robust control
[J]. Journal of Power Sources 2020 , 448 : 227444 .
DOI:10.1016/j.jpowsour.2019.227444
URL
[本文引用: 1]
[7]
杨博 , 俞磊 , 王俊婷 , 等 . 基于自适应蝠鲼觅食优化算法的分布式电源选址定容
[J]. 上海交通大学学报 2021 , 55 (12 ): 1673 -1688 .
[本文引用: 2]
YANG Bo YU Lei WANG Junting et al. Optimal sizing and placement of distributed generation based on adaptive manta ray foraging optimization
[J]. Journal of Shanghai Jiao Tong University 2021 , 55 (12 ): 1673 -1688 .
[本文引用: 2]
[8]
颜志敏 , 王承民 , 郑健 , 等 . 配电网中蓄电池储能系统的价值评估模型
[J]. 电力自动化设备 2013 , 33 (2 ): 57 -61 .
[本文引用: 2]
YAN Zhimin WANG Chengmin ZHENG Jian et al. Value assessment model of battery energy storage system in distribution network
[J]. Electric Power Automation Equipment 2013 , 33 (2 ): 57 -61 .
[本文引用: 2]
[9]
苏海锋 , 胡梦锦 , 梁志瑞 . 基于时序特性含储能装置的分布式电源规划
[J]. 电力自动化设备 2016 , 36 (6 ): 56 -63 .
[本文引用: 2]
SU Haifeng HU Mengjin LIANG Zhirui Distributed generation & energy storage planning based on timing characteristics
[J]. Electric Power Automation Equipment 2016 , 36 (6 ): 56 -63 .
[本文引用: 2]
[10]
章美丹 , 宋晓喆 , 辛焕海 , 等 . 计及网损的配电网电池储能站优化运行策略
[J]. 电网技术 2013 , 37 (8 ): 2123 -2128 .
[本文引用: 2]
ZHANG Meidan SONG Xiaozhe XIN Huanhai et al. Optimal operation strategy of battery energy storagesystem in distribution networks with consideration of power losses
[J]. Power System Technology 2013 , 37 (8 ): 2123 -2128 .
[本文引用: 2]
[11]
LI R WANG W CHEN Z et al. Optimal planning of energy storage system in active distribution system based on fuzzy multi-objective bi-level optimization
[J]. Journal of Modern Power Systems and Clean Energy 2018 , 6 (2 ): 342 -355 .
DOI:10.1007/s40565-017-0332-x
URL
[本文引用: 2]
[12]
贾雨龙 , 米增强 , 刘力卿 , 等 . 分布式储能系统接入配电网的容量配置和有序布点综合优化方法
[J]. 电力自动化设备 2019 , 39 (4 ): 1 -7 .
[本文引用: 1]
JIA Yulong MI Zengqiang LIU Liqing et al. Comprehensive optimization method of capacity configuration and ordered installation for distributed energy storage system accessing distribution network
[J]. Electric Power Automation Equipment 2019 , 39 (4 ): 1 -7 .
[本文引用: 1]
[13]
张忠会 , 雷大勇 , 李俊 , 等 . 基于自适应ε-支配多目标粒子群算法的含SOP的主动配电网源-网-荷-储双层协同规划模型
[J]. 电网技术 2022 , 6, 2199 -2209 .
[本文引用: 2]
ZHANG Zhonghui LEI Dayong LI Jun et al. Source-network-load-storage bi-level collaborative planning model of active distribution network with sop based on adaptive ε-dominating multi-objective particle swarm optimization algorithm
[J]. Power System Technology 2022 , 6, 2199 -2209 .
[本文引用: 2]
[14]
ABU-MOUTI F S EL-HAWARY M E Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm
[J]. IEEE Transactions on Power Delivery 2011 , 26 (4 ): 2090 -2101 .
DOI:10.1109/TPWRD.2011.2158246
URL
[本文引用: 2]
[15]
叶鹏 , 刘思奇 , 关多娇 , 等 . 基于自适应均衡技术的分布式储能聚合模型及评估方法
[J]. 上海交通大学学报 2021 , 55 (12 ): 1689 -1699 .
[本文引用: 2]
YE Peng LIU Siqi GUAN Duojiao et al. An aggregation model and evaluation method of distributed energy storage based on adaptive equalization technology
[J]. Journal of Shanghai Jiao Tong University 2021 , 55 (12 ): 1689 -1699 .
[本文引用: 2]
[16]
SABER H MOEINI-AGHTAIE M EHSAN M Developing a multi-objective framework for expansion planning studies of distributed energy storage systems (DESSs)
[J]. Energy 2018 , 157 : 1079 -1089 .
DOI:10.1016/j.energy.2018.06.081
URL
[本文引用: 2]
[17]
陆立民 , 褚国伟 , 张涛 , 等 . 基于改进多目标粒子群算法的微电网储能优化配置
[J]. 电力系统保护与控制 2020 , 48 (15 ): 116 -124 .
[本文引用: 2]
LU Limin CHU Guowei ZHANG Tao et al. Optimal configuration of energy storage in a microgrid based on improved multi-objective particle swarm optimization
[J]. Power System Protection and Control 2020 , 48 (15 ): 116 -124 .
[本文引用: 2]
[18]
马溪原 , 吴耀文 , 方华亮 , 等 . 采用改进细菌觅食算法的风/光/储混合微电网电源优化配置
[J]. 中国电机工程学报 2011 , 31 (25 ): 17 -25 .
[本文引用: 1]
MA Xiyuan WU Yaowen FANG Hualiang et al. Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm
[J]. Proceedings of the CSEE 2011 , 31 (25 ): 17 -25 .
[本文引用: 1]
[19]
何颖源 , 陈永翀 , 刘勇 , 等 . 储能的度电成本和里程成本分析
[J]. 电工电能新技术 2019 , 38 (9 ): 1 -10 .
[本文引用: 1]
HE Yingyuan CHEN Yongchong LIU Yong et al. Analysis of cost per kilowatt-hour and cost per mileage for energy storage technologies
[J]. Advanced Technology of Electrical Engineering and Energy 2019 , 38 (9 ): 1 -10 .
[本文引用: 1]
[20]
张志义 , 余涛 , 王德志 , 等 . 基于集成学习的含电气热商业楼宇群的分时电价求解
[J]. 中国电机工程学报 2019 , 39 (1 ): 112 -125 .
[本文引用: 1]
ZHANG Zhiyi YU Tao WANG Dezhi et al. Optimal solution of time-of-use price based on ensemble learning for electricity-gas-heat commercial building
[J]. Proceedings of the CSEE 2019 , 39 (1 ): 112 -125 .
[本文引用: 1]
[21]
中华人民共和国国家发展和改革委员会 , 国家能源局 . 解决弃水弃风弃光问题实施方案 [R]. 北京 : 中华人民共和国国家发展和改革委员会, 国家能源局 , 2017 .
[本文引用: 1]
National Development and Reform Commission , National Energy Administration . Implementation plan to solve the problem of water, air and light abandonment [R]. Beijing : National Development and Reform Commission, National Energy Administration , 2017 .
[本文引用: 1]
[22]
林君豪 , 张焰 , 陈思 , 等 . 考虑可控负荷影响的主动配电系统分布式电源优化配置
[J]. 电力自动化设备 2016 , 36 (9 ): 46 -53 .
[本文引用: 1]
LIN Junhao ZHANG Yan CHEN Si et al. Optimal DG allocation considering effect of controllable load for active distribution system
[J]. Electric Power Automation Equipment 2016 , 36 (9 ): 46 -53 .
[本文引用: 1]
[23]
GANDOMI A H YANG X S ALAVI A H Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems
[J]. Engineering with Computers 2013 , 29 (1 ): 17 -35 .
DOI:10.1007/s00366-011-0241-y
URL
[本文引用: 1]
[24]
YANG B WANG J B ZHANG X S et al. Applications of battery/supercapacitor hybrid energy storage systems for electric vehicles using perturbation observer based robust control
[J]. Journal of Power Sources 2020 , 448 : 227444 .
DOI:10.1016/j.jpowsour.2019.227444
URL
[本文引用: 1]
[25]
杨蕾 , 吴琛 , 黄伟 , 等 . 含高比例风光新能源电网的多目标无功优化算法
[J]. 电力建设 2020 , 41 (7 ): 100 -109 .
DOI:10.12204/j.issn.1000-7229.2020.07.013
[本文引用: 1]
为适应新能源大量接入电网的趋势,基于不同时刻的风速、光照强度、温度等气象条件信息,评估出风光新能源的无功调节容量,搭建了含高比例风光新能源参与调控的电网多目标无功优化模型。为快速获得电网中变压器分接头档位调节、无功补偿设备投切、传统发电机组电压调节以及风光的无功输出等控制措施的帕累托最优解集,采用寻优性能高效的多目标樽海鞘群算法（multi-objective salp swarm algorithm, MSSA）进行无功优化求解。为更客观找出电网线损、电压偏差、静态电压稳定裕度等不同目标之间的折中解,采用改进的理想点法进行多目标最优解集决策。最后,利用扩展的IEEE标准9节点和39节点算例进行仿真分析,并引入传统多目标智能优化算法来进行比较验证。仿真结果表明：与其他2种传统多目标智能优化算法相比,所提算法获得的帕累托前沿分布更广、更均匀；利用改进理想点法进行决策之后,可有效降低电网的线损和电压偏差,同时提高了电网的静态电压稳定裕度。
YANG Lei WU Chen HUANG Wei et al. Pareto-based multi-objective reactive power optimization for power grid with high-penetration wind and solar renewable energies
[J]. Electric Power Construction 2020 , 41 (7 ): 100 -109 .
DOI:10.12204/j.issn.1000-7229.2020.07.013
[本文引用: 1]
To adapt the trend of high-penetration renewable energies paralleled in power grid, this paper constructs a multi-objective reactive power optimization for power grid with the controlled participation of high-penetration wind and solar renewable energies. Particularly, the reactive power regulation capacities of renewable energies are evaluated according to the wind speed, solar irradiation, and temperature in different time. To obtain the optimal dispatch scheme of transformer taps, shunt capacitor states, voltage outputs of generators, and reactive power outputs of renewable energies, a multi-objective salp swarm algorithm （MSSA） is employed for the multi-objective reactive power optimization. Then an improved ideal-point based decision method is designed to select a compromise solution among multiple non-dominated points, thus three objectives of power loss, voltage deviation, and static voltage stability margin can be properly balanced. Finally, an extended IEEE 9-bus system and an extended IEEE 39-bus system are used to evaluate the performance of the proposed algorithm compared with conventional multi-objective intelligent optimization algorithms. Simulation results demonstrate that the proposed algorithm can obtain a widely spread and well-distributed Pareto front compared with conventional multi-objective optimization algorithms. Moreover, the improved ideal-point based decision method not only can effectively reduce the power loss and voltage deviation, but also can improve the static voltage stability margin.
[27]
伍忠东 , 高新波 , 谢维信 . 基于核方法的模糊聚类算法
[J]. 西安电子科技大学学报 2004 , 31 (4 ): 533 -537 .
[本文引用: 1]
WU Zhongdong GAO Xinbo XIE Weixin A study of a new fuzzy clustering algorithm based on the kernel method
[J]. Journal of Xidian University 2004 , 31 (4 ): 533 -537 .
[本文引用: 1]
[28]
GOSWAMI S K BASU S K A new algorithm for the reconfiguration of distribution feeders for loss minimization
[J]. IEEE Transactions on Power Delivery 1992 , 7 (3 ): 1484 -1491 .
DOI:10.1109/61.141868
URL
[本文引用: 1]
[29]
RAN F TIMOTHY R ROBERT M Utility-scale photovoltaics-plus-energy storage system costs benchmark
[R]. USA National Renewable Energy Laboratory , 2018 .
[本文引用: 3]
[30]
MIRJALILI S SAREMI S MIRJALILI S M et al. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization
[J]. Expert Systems with Applications 2016 , 47 : 106 -119 .
DOI:10.1016/j.eswa.2015.10.039
URL
[本文引用: 1]
[31]
DURILLO J J NEBRO A J COELLO COELLO C A et al. A comparative study of the effect of parameter scalability in multi-objective metaheuristics
[C]//2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence). Hong Kong China : IEEE , 2008 : 1893 -1900 .
[本文引用: 1]
[32]
王丽萍 , 邱飞岳 . 复杂多目标问题的优化方法及应用 [M]. 北京 : 科学出版社 , 2018 .
[本文引用: 1]
WANG Liping QIU Feiyue Complex multi-objective optimization and it’s applications [M]. Beijing : Science Press , 2018 .
[本文引用: 1]
Optimal sizing and placement of energy storage system in power grids: A state-of-the-art one-stop handbook
1
2020
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey
1
2021
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
蓄电池/超导混合储能系统非线性鲁棒分数阶控制
1
2020
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
蓄电池/超导混合储能系统非线性鲁棒分数阶控制
1
2020
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
Robust fractional-order PID control of supercapacitor energy storage systems for distribution network applications: A perturbation compensation based approach
1
2021
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
Control of SMES systems in distribution networks with renewable energy integration: A perturbation estimation approach
1
2020
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
Applications of battery/supercapacitor hybrid energy storage systems for electric vehicles using perturbation observer based robust control
1
2020
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
基于自适应蝠鲼觅食优化算法的分布式电源选址定容
2
2021
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
基于自适应蝠鲼觅食优化算法的分布式电源选址定容
2
2021
... 电池储能系统(Battery Energy Storage Systems, BESSs)凭借其快速的功率调节和灵活的能量管理能力,可有效解决配电网弃风弃光、电压越限、潮流反向和调峰能力不足等问题[1 ⇓ ⇓ ⇓ ⇓ -6 ] .合理配置BESSs对配电网高效经济运行具有重要意义[7 ] . ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
配电网中蓄电池储能系统的价值评估模型
2
2013
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
配电网中蓄电池储能系统的价值评估模型
2
2013
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
基于时序特性含储能装置的分布式电源规划
2
2016
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
基于时序特性含储能装置的分布式电源规划
2
2016
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
计及网损的配电网电池储能站优化运行策略
2
2013
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
计及网损的配电网电池储能站优化运行策略
2
2013
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (1) 建立基于Pareto的多目标优化模型,以实现BESSs投资成本、配电网电压波动和负荷波动3个目标的最佳权衡.相较于单目标优化[7 -8 ] 和基于线性加权的多目标优化[9 -10 ] ,所提模型不仅综合考虑了BESSs投资经济性和配电网运行可靠性,而且能客观地分配各目标权重,避免因采取主观权重而导致对某一目标产生较大偏好. ...
Optimal planning of energy storage system in active distribution system based on fuzzy multi-objective bi-level optimization
2
2018
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (2) 对BESSs优化配置模型进行双层架构,将建立的多目标优化模型作为外层模型,以求解BESSs选址定容方案;内层模型则以最大化BESSs运营效益为目标求解其充放电运行策略.相较于单层优化和上下层独立循环的双层优化[11 ] ,所构建的双层模型考虑了BESSs规划和运行之间的联系,通过内外层的嵌套循环迭代,保证了优化配置方案的有效性. ...
分布式储能系统接入配电网的容量配置和有序布点综合优化方法
1
2019
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
分布式储能系统接入配电网的容量配置和有序布点综合优化方法
1
2019
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
基于自适应ε-支配多目标粒子群算法的含SOP的主动配电网源-网-荷-储双层协同规划模型
2
2022
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷. ...
基于自适应ε-支配多目标粒子群算法的含SOP的主动配电网源-网-荷-储双层协同规划模型
2
2022
... 目前,国内外诸多学者已对BESSs优化配置模型展开研究.例如,文献[8 -9 ]分别以配电网年净收益最大、年综合成本最小为优化目标,建立了BESSs单目标规划模型.然而,在进行BESSs规划时,需要同时考虑安全性、可靠性、经济性等相互冲突和影响的多个目标,单一目标下的优化难以满足实际工程需要.进而,不少学者利用线性加权等方式将BESSs规划的多个优化目标加权为单个目标进行优化求解[10 -11 ] ,但未能客观地分配各目标权重.文献[12 ]提出了BESSs容量配置和优化布点的双层优化模型,上层以投资经济性确定容量,下层以负荷方差最小进行选址,即在上层优化的结果中再进行下层优化,但实际上未考虑两层优化模型之间的耦合关系.文献[13 ]提出了一种含峰值功率能力的源-网-荷-储双层协同规划模型,有效实现了各层目标函数和决策变量在上下层的优化传递. ...
... (3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷. ...
Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm
2
2011
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... (3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷. ...
基于自适应均衡技术的分布式储能聚合模型及评估方法
2
2021
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... (3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷. ...
基于自适应均衡技术的分布式储能聚合模型及评估方法
2
2021
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... (3) 提出一种孔雀优化算法(Peafowl Optimization Algorithm, POA),并基于Pareto理论设计多目标孔雀优化算法(Multi-Objective Peafowl Optimization Algorithm, MOPOA),分别求解内层和外层模型.在自适应搜索和逼近机制中设计可平衡局部探索和全局搜索的算子,使内层优化有效逼近高质量的最优解,外层优化获得分布广泛且均匀的Pareto非支配解集,从而避免了数学优化方法[13 ] 和传统多目标进化算法[14 -15 ] 存在的易陷入局部最优等固有缺陷. ...
Developing a multi-objective framework for expansion planning studies of distributed energy storage systems (DESSs)
2
2018
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
基于改进多目标粒子群算法的微电网储能优化配置
2
2020
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
基于改进多目标粒子群算法的微电网储能优化配置
2
2020
... 此外,鉴于BESSs的优化配置是一个多变量、且含离散变量的复杂非线性多目标优化问题,多目标进化算法能够比传统的数学优化方法[14 ] 更有效地获得全局最优解[15 ] .文献[16 ]采用非支配解排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II, NSGAII)求解BESSs多目标规划模型,但该算法交叉变异操作的随机性较强.文献[17 ]提出改进的多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解BESSs安装位置和容量,然而该算法惯性权重的取值缺乏指导,寻优性能稍差. ...
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
采用改进细菌觅食算法的风/光/储混合微电网电源优化配置
1
2011
... 式中:C inv 为单台BESS的固定投资成本;N BESS 为BESSs的安装数量;E BESS, n P BESS, n n 台BESSs的配置容量和功率;a 和b 分别为BESSs的单位功率成本和不同充电倍率(C rate )下的单位容量成本;μ CRF 为年资金回收率;y 为BESSs的使用年限,本文取y =10;r 为折现率,采用加权平均资金成本[18 ] 计算.需说明的是,在目标函数计算中,把一年分为多个典型场景计算,同时考虑BESSs的投资运行年限,将所有资金折算成现值. ...
采用改进细菌觅食算法的风/光/储混合微电网电源优化配置
1
2011
... 式中:C inv 为单台BESS的固定投资成本;N BESS 为BESSs的安装数量;E BESS, n P BESS, n n 台BESSs的配置容量和功率;a 和b 分别为BESSs的单位功率成本和不同充电倍率(C rate )下的单位容量成本;μ CRF 为年资金回收率;y 为BESSs的使用年限,本文取y =10;r 为折现率,采用加权平均资金成本[18 ] 计算.需说明的是,在目标函数计算中,把一年分为多个典型场景计算,同时考虑BESSs的投资运行年限,将所有资金折算成现值. ...
储能的度电成本和里程成本分析
1
2019
... 式中:ρ om 为运维系数,即BESSs年运维费用占设备投资成本的比率,约为1%~10%[19 ] . ...
储能的度电成本和里程成本分析
1
2019
... 式中:ρ om 为运维系数,即BESSs年运维费用占设备投资成本的比率,约为1%~10%[19 ] . ...
基于集成学习的含电气热商业楼宇群的分时电价求解
1
2019
... t [20 ] ; P c h a , n ( t ) P d i s , n ( t ) n t 时段内的充电和放电功率;T =24 h. ...
基于集成学习的含电气热商业楼宇群的分时电价求解
1
2019
... t [20 ] ; P c h a , n ( t ) P d i s , n ( t ) n t 时段内的充电和放电功率;T =24 h. ...
1
2017
... 式中:R cur,max 为最大年弃风弃光率,设为5%[21 ] ;R cur 为年弃风弃光率,且 ...
1
2017
... 式中:R cur,max 为最大年弃风弃光率,设为5%[21 ] ;R cur 为年弃风弃光率,且 ...
考虑可控负荷影响的主动配电系统分布式电源优化配置
1
2016
... 式中: Δ P g r i d ( t ) P U p p u p p [22 ] . ...
考虑可控负荷影响的主动配电系统分布式电源优化配置
1
2016
... 式中: Δ P g r i d ( t ) P U p p u p p [22 ] . ...
Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems
1
2013
... 在模型内层,采用寻优性能良好的POA求解最优的BESSs充放电运行策略,并在算法内部调用Matpower工具箱采用快速解耦算法进行配电网潮流计算.POA的算法原理和验证参见文献[23 ],本文仅对算法的寻优机制进行简述. ...
Applications of battery/supercapacitor hybrid energy storage systems for electric vehicles using perturbation observer based robust control
1
2020
... 幼孔雀自适应搜索食物源.幼孔雀向雄孔雀移动的同时借助Levy飞行机制[24 ] 在搜索空间进行随机搜索: ...
含高比例风光新能源电网的多目标无功优化算法
1
2020
... 在模型外层,设计基于Pareto的MOPOA求解BESSs的最佳选址定容方案.首先,根据式(25)~(32)逐代更新外层孔雀种群的位置,以不断更新BESSs选址定容方案的Pareto解集.进而,采用改进理想点决策(Improved Ideal Point Based Decision, IIPBD)[25 ] 方法决策BESSs最佳选址定容方案. ...
含高比例风光新能源电网的多目标无功优化算法
1
2020
... 在模型外层,设计基于Pareto的MOPOA求解BESSs的最佳选址定容方案.首先,根据式(25)~(32)逐代更新外层孔雀种群的位置,以不断更新BESSs选址定容方案的Pareto解集.进而,采用改进理想点决策(Improved Ideal Point Based Decision, IIPBD)[25 ] 方法决策BESSs最佳选址定容方案. ...
Equilibrium optimizer: A novel optimization algorithm
2
2020
... 在算法迭代过程中,采用外部归档集来存储Pareto非支配解集.MOPOA-POA在每次迭代中获得的新非支配解集,须逐一与原非支配解集进行比较并更新外部归档集[26 ] :① 若新解支配归档集里的某一个或多个解,则将归档集中被支配的解替换为新解;② 若归档集里至少有一个解支配新解,则放弃新解;③ 若新解与归档集里的所有解均互不支配,则将新解放入外部归档集. ...
... 由IEEE-33节点系统参数[26 ] 可知,节点6、7、23、24、29为系统重负荷节点,所提算法将2台BESSs分别配置在节点7和节点23,以满足重负荷地区的电能需要,并尽可能消纳新能源出力.特别地,安装在线路上游的BESS容量最大,可以更好地提升节点电压、降低网损.另外,所配置BESSs的充电倍率均为4C ,虽然增加了容量成本,但高充电倍率下电池的恒流充电时间更短,更能满足电网对BESSs的响应要求,也能较大发挥BESSs的充放电能力,从而获得较高的运营收益.然而,较高的充电倍率也会加速电池的容量衰减快慢,影响电池寿命,而本文未考虑BESSs的循环寿命损耗,乃不妥之处. ...
基于核方法的模糊聚类算法
1
2004
... 考虑负荷、风电和光伏出力的不确定性,采用多个典型日场景下的负荷、风电和光伏出力曲线代表全年,更好地反映负荷和新能源在全年的不确定性.首先,采用一种模糊核C -均值聚类算法[27 ] 处理云南省某地的年历史数据,分别得到负荷、风电和光伏的典型日曲线,如图2 所示.进而,综合考虑负3种曲线的相关性,通过场景组合得到4种典型场景,每种场景的组合方式及对应天数如表1 所示. ...
基于核方法的模糊聚类算法
1
2004
... 考虑负荷、风电和光伏出力的不确定性,采用多个典型日场景下的负荷、风电和光伏出力曲线代表全年,更好地反映负荷和新能源在全年的不确定性.首先,采用一种模糊核C -均值聚类算法[27 ] 处理云南省某地的年历史数据,分别得到负荷、风电和光伏的典型日曲线,如图2 所示.进而,综合考虑负3种曲线的相关性,通过场景组合得到4种典型场景,每种场景的组合方式及对应天数如表1 所示. ...
A new algorithm for the reconfiguration of distribution feeders for loss minimization
1
1992
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
Utility-scale photovoltaics-plus-energy storage system costs benchmark
3
2018
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
... BESSs的相关参数[29 ] ...
... Parameters of BESSs[29 ] ...
Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization
1
2016
... 采用扩展的IEEE-33节点配电网测试系统[28 ] 进行仿真分析,以验证所提方法进行BESSs优化配置的有效性,其拓扑结构如图3 所示.其中,G为平衡节点,可向配电网提供缺额功率,也可吸收配电网的多余功率,以保证功率平衡.考虑高比率新能源的渗透,在节点9、20、25分别接入风电1号、2号、3号,在节点28接入光伏1号.仅考虑新能源场站的有功输出,不计无功.电网主要参数为系统基准容量10 MV·A,总负荷功率(3.715+j2.3) MV·A,风电1号、2号、3号有功功率1.2 MW,光伏1号有功功率2.5 MW.选择锂电池作为BESSs的储能元件,相关参数如表2 所示[29 ] .为验证所提MOPOA-POA的优越性,仿真算例引入基于MOPSO[17 ] 、NSGAII[16 ] 和MOGWO[30 ] 设计的双层MOPSO-PSO、NSGAII-GA和MOGWO-GWO进行对比.4种算法的基本参数设为一致,即内、外层最大迭代次数均设为100,内、外层种群规模均设为100,外部归档集规模设为20.此外,所有算法均在主频为2.80 GHz 的Intel® CoreTM i5-8400 CPU、内存为8 GB 的计算机和MATLAB 2018b环境下进行优化计算,并调用Matpower工具箱进行潮流计算. ...
A comparative study of the effect of parameter scalability in multi-objective metaheuristics
1
2008
... 图4 和图5 (a)分别为4种算法在IEEE-33节点系统获得的两目标和三目标Pareto前沿.需说明的是,不同算法的Pareto前沿由其Pareto非支配解集中的解构成.从图中可知,在同样的迭代次数、种群数量及外部归档集规模条件下,MOPOA-POA获得的两目标和三目标Pareto前沿明显比其他3种算法延伸范围更广、分布更均匀.另外,将4种算法分别得到的Pareto非支配解集对应的目标值全部组合起来,确定该组合解集的Pareto前沿,以此作为所有算法求解该多目标优化问题的近似Pareto最优前沿[31 ] .比较不同算法的Pareto前沿与近似Pareto最优前沿的差距,可知由MOPOA-POA求得的Pareto前沿与该多目标优化问题的近似Pareto最优前沿重合度更高,因此本文所提算法的多目标优化性能较优.图5 (b)为采用IIPBD方法从 ...
1
2018
... 另外,采用世代距离(Generational Distance, GD)、反转世代距离(Inverted Generational distance, IGD)、空间分布(Spacing, SP)、广泛性、纯粹多样性(Pure Diversity, PD)、分布度指标(Diversity Metric, DM)、超体积(Hyper Volume, HV)定量评估算法的Pareto解集性能[32 ] ,结果如表4 所示.可知, MOPOA-POA的GD和IGD指标最低, ...
1
2018
... 另外,采用世代距离(Generational Distance, GD)、反转世代距离(Inverted Generational distance, IGD)、空间分布(Spacing, SP)、广泛性、纯粹多样性(Pure Diversity, PD)、分布度指标(Diversity Metric, DM)、超体积(Hyper Volume, HV)定量评估算法的Pareto解集性能[32 ] ,结果如表4 所示.可知, MOPOA-POA的GD和IGD指标最低, ...
