基于PCA-ELM的红外多光谱辐射测温

doi:10.16183/j.cnki.jsjtu.2020.027

基于PCA-ELM的红外多光谱辐射测温

席剑辉, 姜瀚, 陈博, 傅莉^,

沈阳航空航天大学自动化学院, 沈阳 110136

Infrared Multispectral Radiation Temperature Measurement Based on PCA-ELM

XI Jianhui, JIANG Han, CHEN Bo, FU Li^,

School of Automation, Shenyang Aerospace University, Shenyang 110136, China

通讯作者: 傅莉,女,教授,电话(Tel.): 15840355071;E-mail:ffulli@163.com.

责任编辑: 石易文

收稿日期: 2020-01-22

基金资助:

国际科技合作计划项目(WQ20122100063)
国家自然科学基金青年基金资助项目(61503256)
辽宁省自然科学基金项目(2015020069)
沈阳市科技创新团队项目(src201204)

Received: 2020-01-22

作者简介 About authors

席剑辉(1975-),女,辽宁省沈阳市人,副教授,主要研究方向为复杂系统模型辨识、故障检测与诊断、红外辐射测试与分析等。

摘要

在目标发射率未知的情况下,建立一种基于主元分析(PCA)与极限学习机(ELM)相结合的红外多光谱测温方法.分析目标温度与辐射亮度谱的非线性数学模型,确定初始输入向量包含温度估计所需的充分信息;引入PCA方法从输入向量中提取相互独立的主元成分,降低神经网络输入维数;基于ELM网络对样本数据充分学习,最终建立PCA-ELM目标红外测温模型.利用黑体和未知发射率材料涂层目标作为测试目标源,验证该方法的有效性.

关键词： 主元分析; 极限学习机; 多光谱测温; 辐射亮度

Abstract

In the case of unknown target emissivity, an infrared multispectral radiation temperature measurement method based on principal component analysis (PCA) and extreme learning machine (ELM) is established. The nonlinear mathematic model of target temperature and radiance spectrum is analyzed to find a set of initial input vectors, which include sufficient information to estimate temperature. The PCA method is used to extract the independent principle components in input vectors. This method can also reduce the input dimension for neural network. Based on ELM network, the sample data is sufficiently learned to build the target infrared temperature measurement model by PCA-ELM. The effectiveness of the proposed method is verified by using the blackbody and the coating material with unknown emissivity as test target sources.

Keywords： principal component analysis (PCA); extreme learning machine (ELM); multispectral thermometry; radiance

PDF (1988KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

席剑辉, 姜瀚, 陈博, 傅莉. 基于PCA-ELM的红外多光谱辐射测温[J]. 上海交通大学学报（自然版）, 2021, 55(7): 891-898 doi:10.16183/j.cnki.jsjtu.2020.027

XI Jianhui, JIANG Han, CHEN Bo, FU Li. Infrared Multispectral Radiation Temperature Measurement Based on PCA-ELM[J]. Journal of shanghai Jiaotong University, 2021, 55(7): 891-898 doi:10.16183/j.cnki.jsjtu.2020.027

红外辐射测量得到的目标热辐射通量与目标温度以及材料发射率紧密相关,所以红外测温通常需要已知目标的发射率^[1,2].常用的测温方法主要有光谱极值法、全辐射测温法和亮度测温法等^[3,4,5].光谱极值法用于当目标为黑体或灰体时,发射率为一个小于或等于1的固定常数.通过测量辐射峰值点处波长,根据Wien位移定律计算温度.全辐射测温法依据Stefan-Boltzmann定律,通过测量目标的总辐射能量计算目标温度,只能通过局部波段能量近似获得.亮度测温法通过测量目标在给定波长下的辐射亮度值,获得与目标光谱辐射亮度相等的黑体温度,称为亮温,再根据亮温和发射率求得目标温度.

但在实际测量中,发射率与目标材料的成分、表面状况、所处的温度和考察的波长等因素均有关,无法建立完备的目标发射率数据库,因此在测温过程中,目标的发射率往往都是未知的.目前,针对目标发射率未知情况下的红外测温方法一般有比色测温法^[6,7] 以及多光谱测温法^[8,9].比色测温法是通过测量两个波段的辐射能量之比计算温度的.通常选取两个相近波段,认为两者的发射率近似相等可以互相消除.若所选波段的发射率发生较大变化时,其相应的测温误差也会较大.多光谱测温法通过测量多个目标光谱的辐射亮度建立测温模型.最初,Svet等^[10]引入发射率非线性模型,建立一组与模型未知参数个数相等的方程组,通过求解方程组估计目标温度和光谱发射率.所建立的方程组数量与结构对估计结果的影响较大,线性方程难以表征目标温度与红外光谱信息之间的强非线性关系.建立非线性高阶方程组会导致方程组维数迅速上升,对样本数量和求解算法提出更高的要求. 测温过程中,大气、背景等复杂影响因子要求模型辨识方法应该具有良好的稳健性和适应性.近年来,自适应的智能模型辨识方法经常被用于多光谱测温^[11,12].

神经网络通过充分的样本训练自适应学习样本中隐含的非线性关系,进而建立测温模型,建模过程不需要预知目标光谱发射率^[12,13,14].本文主要采用一种动态神经网络极限学习机(ELM),学习在不同温度情况下,目标辐射亮度谱与温度之间的非线性映射关系;引入主元分析(PCA)方法对输入向量降维且保留主元特征,减弱输入样本中的冗余信息,避免网络过度学习,提高建模精度.

1 目标辐射温度建模

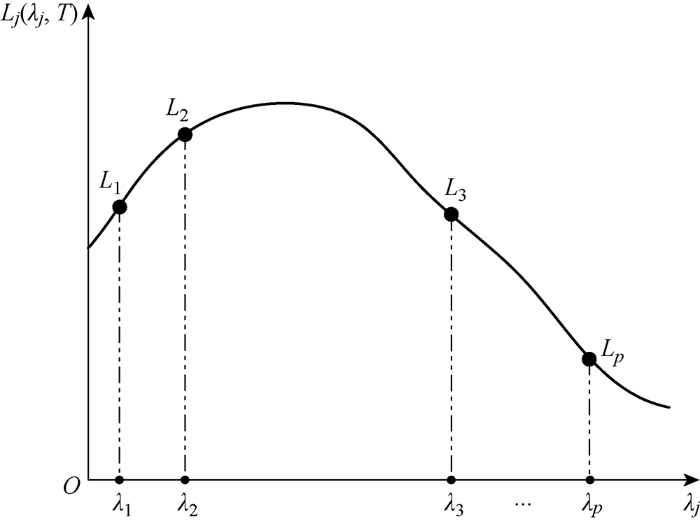
当温度为T时,目标辐射亮度的典型曲线如图1所示.其中:λ_j为波长;L_j (λ_j, T) 为辐射亮度.当λ_j 分别取固定值为λ₁,λ₂,…,λ_p时,固定温度下对应的辐射亮度值分别为L₁,L₂,…,L_p.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 当温度为T时的典型目标辐射亮度曲线

Fig.1 Radiance curve of a typical target at a temperature of T

由Planck定律和光谱发射率定义可得,当温度为T时,目标的辐射亮度为

(1)L_j(λ_j,T)=ε(λ_j,T)

\frac{C_{1}}{π λ_{j}^{5}} \frac{1}{e^{C_{2} / λ_{j} T} - 1}

式中:ε(λ_j, T)为光谱发射率;C₁和C₂分别为第一热辐射常数、第二热辐射常数.在同一温度T下,不同波长λ₁,λ₂,…,λ_p对应的亮度为

(2)

\begin{array}{l} L_{1} = ε (λ_{1}, T) \frac{C_{1}}{π λ_{1}^{5}} \frac{1}{e^{C_{2} / λ_{1} T} - 1} \\ L_{2} = ε (λ_{2}, T) \frac{C_{1}}{π λ_{2}^{5}} \frac{1}{e^{C_{2} / λ_{2} T} - 1} \\  \\ L_{p} = ε (λ_{p}, T) \frac{C_{1}}{π λ_{p}^{5}} \frac{1}{e^{C_{2} / λ_{p} T} - 1} \end{array}\}

式中:ε(λ₁, T),ε(λ₂, T),…,ε(λ_p, T)为未知的光谱发射率,只与T和λ_j有关.因此,L₁,L₂,…,L_p可以看成p个关于温度T和λ_j的隐函数,通过选用固定波长下的多光谱亮度信息,就可以对温度进行估计,建立基于多光谱亮度信息的目标温度模型.

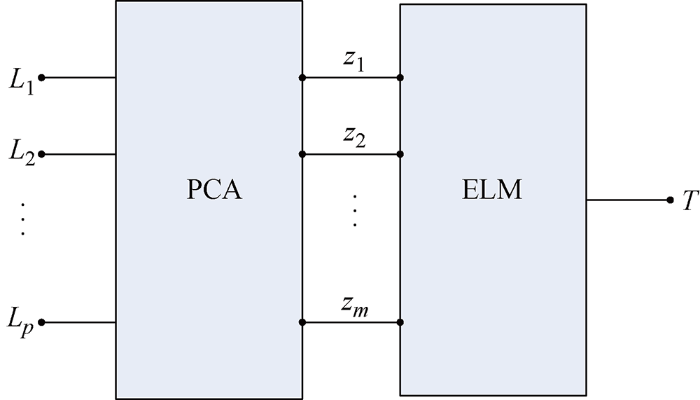
由式(2)可知:① 方程组具有强非线性,常规模型辨识方法很难获取亮度谱与温度之间的关系;② 方程组个数p不少于等式右边展开后未知参数的个数,p值过大时,式(2)求解困难.神经网络不需要具体知道系统动态特性,无需建立初始数学模型,尤其适用于难以用确定数学模型表达的非线性系统建模^[13].所设计的测温模型结构如图2所示,其中z₁,z₂,…,z_m (m<p)为主元成分.模型输入端为L₁,L₂,…,L_p,输出端为T.通过在已知温度下测量亮度谱曲线,获取输入输出样本对;再利用神经网络的强学习能力寻找输入输出间的潜在规律.为使输入包含足够的建模信息,输入亮度L₁,L₂,…,L_p往往取值密集,造成输入维数p数值高、建模困难.输入变量之间存在较强的相关性和冗余信息,导致网络学习精度下降,可泛化性弱.因此,在神经网络输入端引入PCA层提取输入变量中的主元成分z₁,z₂,…,z_m (m<p),通过降低输入维数,以提高建模精度.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 测温模型结构框图

Fig.2 Structure diagram of temperature measurement model

2 PCA-ELM红外光谱测温方法

在不同温度T下测量光谱亮度,总共测量n个不同温度.设第k个温度下,对应p个波长的光谱辐射亮度输入为L(k)=[L₁(k) L₂(k) … L_p(k)]^T (k=1,2,…,n).若输入变量间方差越大,相关性越小,则越具有好的区分能力.PCA 方法正是利用这一规律,以确定具有较大方差的主元变量为目标,对输入变量进行线性组合,使获得的输入向量具有更好的模式区分能力.

ELM是一种单隐层前馈网络,网络结构简单,输入层与隐含层连接权值以及隐含层神经元阈值在训练过程中无需调整,训练时间快,因此本文神经网络选用ELM神经网络.

2.1 PCA的原理和步骤

设有n个不同温度下的目标辐射亮度向量,每个向量包含p个不同波长下对应的亮度值,构成一个p×n阶的矩阵Λ,

(3)Λ=

{[\begin{array}{l} L_{1} (1) & L_{1} (2) & \dots & L_{1} (n) \\ L_{2} (1) & L_{2} (2) & \dots & L_{2} (n) \\  &  &  &  \\ L_{p} (1) & L_{p} (2) & \dots & L_{p} (n) \end{array}]}_{p \times n}

令z(k)=[z₁(k) z₂(k) … z_m(k)]^T (m<p),为Λ中蕴含的主元变量,为便于表达,把变量k省略,则不同温度下,都满足下式:

(4)

\begin{array}{l} z_{1} = a_{11} L_{1} + a_{12} L_{2} + \dots + a_{1 p} L_{p} \\ z_{2} = a_{21} L_{1} + a_{22} L_{2} + \dots + a_{2 p} L_{p} \\   \\ z_{m} = a_{m 1} L_{1} + a_{m 2} L_{2} + \dots + a_{mp} L_{p} \end{array}\}

式中: $a_{i 1}^{2}$ + $a_{i 2}^{2}$ +…+ $a_{ip}^{2}$ =1 (i=1,2,…,m).确定原则为^[15]:① z_i与z_j (i≠j,i,j=1,2,…,m)相互无关;② z₁为L₁,L₂,…,L_p一切线性组合中的方差最大者;③ z₂为与z₁不相关的L₁,L₂,…,L_p所有线性组合中方差最大者;④ z_m为与z₁,z₂,…,z_m_-1均不相关的L₁,L₂,…,L_p所有线性组合中方差最大者.则新输入变量z₁,z₂,…,z_m称为原输入变量L₁,L₂,…,L_p的第1,2,…,m个主成分.

从以上分析可以看出,主成分分析的实质是确定权值a_ij (i=1,2,…,m;j=1,2,…,p),分别为相关矩阵m个较大特征值所对应的特征向量.PCA的步骤如下^[15,16]:

(1) 将原始数据标准化.

(2) 建立变量的相关系数矩阵R=[r_ij]_p_×_p.

(5)r_ij=

\frac{\sum_{k = 1} (L_{i} (k) - {\bar{L}}_{i}) (L_{j} (k) - {\bar{L}}_{j})}{\sqrt[]{\sum_{k = 1} (L_{i} (k) - {\bar{L}}_{i})^{2} \sum_{k = 1} (L_{j} (k) - {\bar{L}}_{j})^{2}}}

式中: ${\bar{L}}_{i}$ 为L_i的均值; ${\bar{L}}_{j}$ 为L_j的均值.

(3) 求R的特征根λ₁≥λ₂≥…≥λ_p>0及其相应的单位特征向量.

a₁= ${[\begin{array}{l} a_{11} & a_{12} & \dots & a_{1 p} \end{array}]}^{T}$

a₂= ${[\begin{array}{l} a_{21} & a_{22} & \dots & a_{2 p} \end{array}]}^{T}$



a_p= ${[\begin{array}{l} a_{p 1} & a_{p 2} & \dots & a_{p p} \end{array}]}^{T}$

(4) 计算前m个特征值的累计贡献率γ_m.

(6)γ_m=

\frac{\sum_{k = 1} λ_{k}}{\sum_{k = 1} λ_{k}}

(5) 一般当γ_m>85%~95%时,可得m个主成分z_i,令i=1,2,…,m

(7)z_i=a_i₁L₁+a_i₂L₂+…+a_ipL_p

2.2 ELM的原理

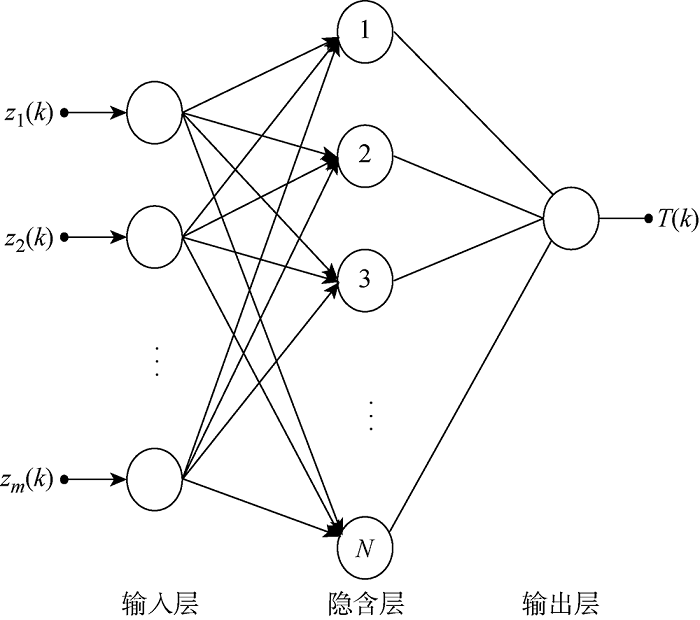
ELM^{[14,15,16,17]}是一种单隐层神经网络,可以随机初始化输入权重和偏置,网络结构图如图3所示,其中N为隐含层神经个数.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 ELM网络结构图

Fig.3 Structure of ELM network

对第k个学习样本,有网络输入为z(k)=[z₁(k) z₂(k) … z_m(k)]^T,网络输出为对应该输入的第k个温度T(k).共测量n个温度,则有k=1,2,…,n;m为PCA确定的主元维数.ELM网络隐含层的输出为

(8)T(k)=

\sum_{l = 1}

β_lg(W_l·z(k)+b_l)

式中:g(·)为激活函数,ELM对激活函数没有特别要求,常见的激活函数有sigmoid函数和tanh函数;W_l为输入权重;β_l为隐含层第l个神经元到输出的权重;b_l为隐含层第l个神经元的阈值.单隐层神经网络的训练目标是要使得拟合的误差最小,即网络输出T(k)与理想输出O(k)差的范数趋向于0,可表示为

(9)

\sum_{k = 1}

‖O(k)-T(k)‖=0

寻找b_l、W_l、β_l使得

(10)

\sum_{l = 1}

β_lg(W_l·z(k)+b_l)=O(k)

设Y为隐含层节点输出矩阵,通过矩阵初等变换得到矩阵的秩为h,则矩阵Y可分解为

(11)Y(W₁…W_N,b₁…b_N,z(1)…z(n))=

[\begin{array}{l} g (W_{1} \cdot z (1) + b_{1}) & \dots & g (W_{N} \cdot z (1) + b_{N}) \\  & ⋱ &  \\ g (W_{1} \cdot z (n) + b_{1}) & \dots & g (W_{N} \cdot z (n) + b_{N}) \end{array}]

=FG

式中:F为n×h满秩矩阵;G为h×N满秩矩阵.

最终找到 ${\hat{W}}_{l}$ , ${\hat{b}}_{l}$ , ${\hat{β}}_{l}$ 使得式(9)取最小,即等价于求解最小化损失函数:

(12)E=

\sum_{k = 1} {[\sum_{l = 1} {\hat{β}}_{l} g ({\hat{W}}_{l} \cdot z (k) + {\hat{b}}_{l}) - O (k)]}^{2}

输入权重 ${\hat{W}}_{l}$ 和阈值 ${\hat{b}}_{l}$ 可随机确定,即可求出隐含层的输出矩阵Y,不需要不断地调整迭代参数.单隐层神经网络便转化成了求解线性系统,可表示为Y $\hat{β}$ =T(13)式中: $\hat{β}$ 为输出权重矩阵;T为ELM网络的温度输出向量,由T(k)组成.由式(11)可唯一确定Y的Moore-Penrose逆Y⁺:

(14)Y⁺=G^H(GG^H)^-1(F^HF)^-1F^H

式中:G^H和F^H为G和F的共轭转置矩阵,则有:

(15)

\hat{β}

=Y⁺T

3 具体实例

实验采用加拿大ABB BOMEN 的MR170 型光谱辐射计,测量目标在不同温度下的辐射特性.辐射计的分辨率为32/cm,探测器的光谱范围为3~14μm波段.

3.1 黑体测温及验证

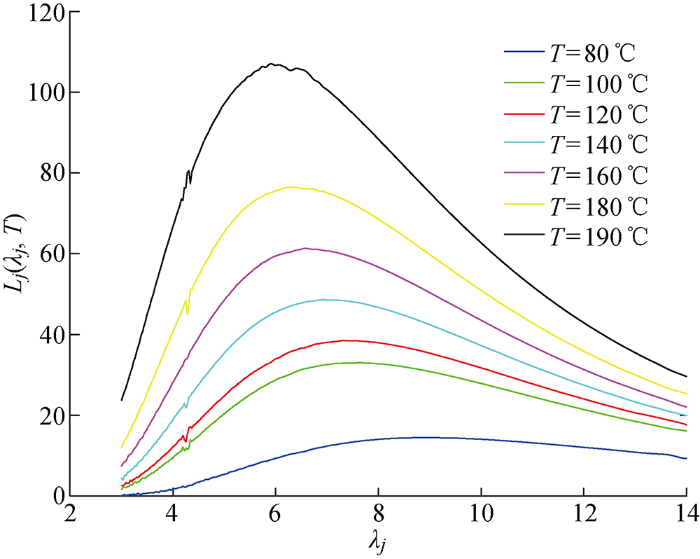
实验室现有3种不同型号的黑体,发射率出厂值以及测温范围略有不同.黑体A的发射率为0.98、有效测温范围为50~250℃;黑体B的发射率为0.96、有效测温范围为300~600℃;黑体D的发射率为0.99、有效测温范围为700~1200℃.分别将3种黑体作为测试目标源,利用光谱辐射计分别测量不同温度下的辐射特性,得到43组样本数据,其中黑体A有28组、黑体B有9组、黑体D有6组.3种黑体的发射率有差异、温度范围没有交叉,现将这3种黑体的数据同时做为训练样本,验证所提方法的测温精度.测试曲线采用文献[13]的方法进行校准补偿,最终得到测量波段光谱亮度样本,随机选取7组不同温度下的亮度曲线如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 黑体在不同温度下的光谱辐射亮度

Fig.4 Spectral radiance of blackbody at different temperatures

光谱亮度会受到杂散辐射、大气吸收散射等影响,导致某些固定波段内的值会产生较大震荡.选择测温训练样本时,可以避开这些波段.在同一温度下,选择有效辐射亮度值141个,样本可对测量波段全覆盖,使得构成的输入向量中包含温度估计需要的光谱信息,最终获取样本共43组,部分样本数据如表1所示.

表1 黑体光谱亮度样本

Tab.1 Samples of spectral radiance from blackbody

T/℃	L₁/(W·m^-2· sr^-1·μm^-1)	L₂/(W·m^-2· sr^-1·μm^-1)	…	L₁₄₁/(W·m^-2· sr^-1·μm^-1)
80	0.629	0.671	…	17
85	0.755	0.781	…	17
︙	︙	︙	…	︙
1300	24158	23740	…	416

新窗口打开| 下载CSV

在不同温度段随机选取35组光谱亮度做为训练样本,可得式(3)的亮度矩阵Λ是一个35×141阶矩阵.根据PCA计算主元成分,获得的特征值和特征向量如表2所示.

表2 黑体光谱亮度PCA结果

Tab.2 PCA results of spectral radiance of blackbody

特征值	特征向量
λ₁=138.7186	a₁=[ $\begin{array}{l} 0.0820 & 0.0821 & \dots & 0.0845 \end{array}$ ]^T
λ₂=2.2762	a₂=[ $\begin{array}{l} 0.1713 & 0.1694 & \dots & - 0.0621 \end{array}$ ]^T
λ₃=0.0051	a₃=[ $\begin{array}{l} 0.2696 & 0.2490 & \dots & 0.0834 \end{array}$ ]^T
︙	︙
λ₁₄₁=0	a₁₄₁=[ $\begin{array}{l} 0.0602 & - 0.0630 & \dots & - 0.2857 \end{array}$ ]^T

新窗口打开| 下载CSV

由式(6)可知,计算前两个特征值的贡献率γ₁=98.3%,γ₂=1.614%,累计贡献率达99.9%,确定主成分为2,得到降维后的网络输入为z₁(k)=a₁·L(k),z₂(k)=a₂·L(k)(k=1,2,…,n).

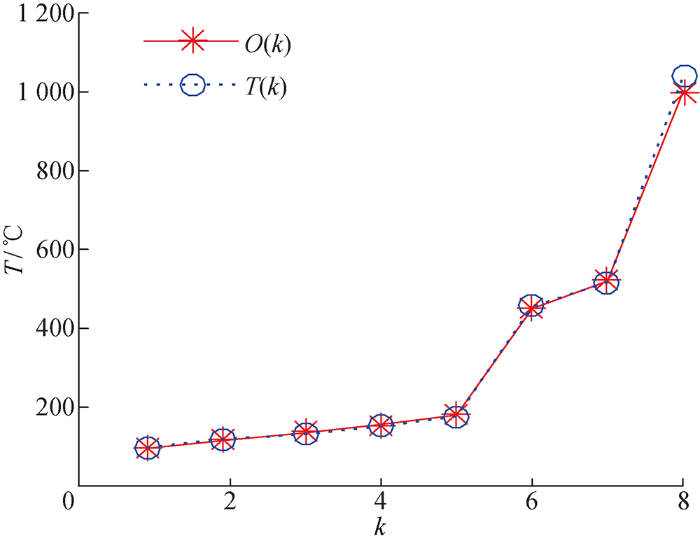
将z₁和z₂输入ELM网络,网络输出为T,隐含层节点数为8个.训练结束后,将8组测试样本输入网络得到的验证结果如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 黑体温度的ELM网络输出值与实测值比较

Fig.5 Comparison of blackbody temperature between estimated values obtained by ELM network and practical values

由图5中可以看出,ELM网络输出的温度与真实温度非常相近,且精度较高.具体结果如表3所示.其中,T₁为真实温度;T₂为网络输出温度; $\frac{|O (k) - T (k)|}{O (k)}$ 为温度估计相对误差; $\bar{ε}$ 为平均发射率.由表3可知,温度估计最大相对误差为3.58%.基于温度测量结果可进一步估计目标当前温度下的光谱发射率.某一温度T下,令j=1,2,…,p,一般目标接近朗伯体,光谱发射率ε(λ_j, T)与方向无关,可表示为

(16)ε(λ_j,T)=

\frac{L_{j} (λ_{j}, T)}{L_{bb} (λ_{j}, T)}

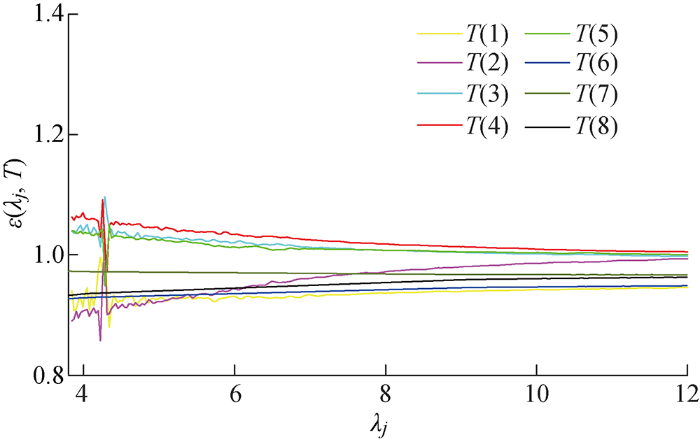
式中:L_bb(λ_j,T)为温度T时的标准黑体光谱辐射亮度.理想黑体光谱发射率不随波长变化,表现为常值,所测黑体为哈尔滨工业大学自动检测与过程控制系统研究所研制的面源黑体,发射率出厂值为0.98.根据表3得到的温度可获得理想黑体辐射亮度,根据式(16)计算的光谱发射率如图6所示,其中T(1),T(2),…,T(8)为8个温度.由图6可知,不同温度下光谱发射率在0.98上下浮动,且比较恒定.计算测量波段的平均发射率 $\bar{ε}$ 并将其与真实值0.98进行比较, $\frac{|0.98 - \bar{ε}|}{0.98}$ 为计算相对误差.由表3可以看出,平均发射率的最大相对误差为4.3%,说明所提方法可以实现目标温度与光谱发射率的同步估计,且可达到较高的精度.

表3 黑体的测温结果及其相对误差

Tab.3 Temperature measurement results of blackbody and its relative errors

T₁/℃	T₂/℃	$\frac{\|O (k) - T (k)\|}{O (k)}$ /%	$\bar{ε}$	$\frac{\|0.98 - \bar{ε}\|}{0.98}$ /%
95	97.4762	2.61	0.9318	4.8
115	119.1212	3.58	0.9673	1.3
135	131.8413	2.34	1.0110	3.2
155	150.7401	2.75	1.0217	4.3
180	176.3031	2.05	1.0151	3.6
450	455.9431	1.32	0.9410	4.0
520	517.7082	0.44	0.9688	1.1
1000	1025.3000	2.53	0.9523	2.8

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 黑体测试样本的光谱发射率估计

Fig.6 Estimation of spectral emissivity for testing samples of blackbody

通过黑体实验可以验证所提测温方法的合理性,且测温范围广,主要取决于所选网络训练样本的温度范围.

3.2 目标涂层的测温及验证

将所提方法应用于飞机机身表面涂层的温度估计,如图7所示.涂层温度通过外接温度控制器控制,利用光谱辐射计测量表面涂层的辐射特性,得到41组不同温度下的光谱亮度辐射数据,温度范围为80~180 ℃.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 钢板涂层目标

Fig.7 Steel plate coating target

与黑体实验相同,在每条温度曲线上,选取141个不同波长对应的辐射亮度值作为初始输入向量.部分样本数据如表4所示.

表4 目标涂层光谱亮度部分样本

Tab.4 Samples of spectral radiance from coating target

T/℃	L₁/(W·m^-2· sr^-1·mm^-1)	L₂/(W·m^-2· sr^-1·mm^-1)	…	L₁₄₁/(W·m^-2· sr^-1·mm^-1)
80	0.516	0.567	…	13.852
83	0.562	0.614	…	14.117
︙	︙	︙	︙	︙
180	2.417	2.233	…	17.000

新窗口打开| 下载CSV

随机选取34组训练样本,可得式(3)的亮度矩阵Λ是一个34×141阶矩阵.根据PCA计算主元成分,得到特征值和特征向量如表5所示.计算累计贡献率,确定主成分为1,得到降维后的网络输入为z₁(k)=a₁·L(k),k=1,2,…,n.得到第k个样本降维后的输入变量为

表5 目标涂层光谱亮度PCA结果

Tab.5 PCA results of spectral radiance of coating target

特征值	特征向量
λ₁=125.3228	a₁=[ $\begin{array}{l} 0.0475 & 0.0386 & \dots & 0.0796 \end{array}$ )^T
λ₂=12.0106	a₂=[ $\begin{array}{l} 0.1931 & 0.2276 & \dots & - 0.0362 \end{array}$ ]^T
λ₃=2.6217	a₃=[ $\begin{array}{l} 0.2838 & 0.2372 & \dots & - 0.2458 \end{array}$ ]^T
︙	︙
λ₁₄₁=0	a₁₄₁=[ $\begin{array}{l} 0.0007 & - 0.0020 & \dots & 0.5271 \end{array}$ ]^T

新窗口打开| 下载CSV

z₁(k)=0.0475L₁(k)+0.0386L₂(k)+…+ 0.0796L₁₄₁(k)

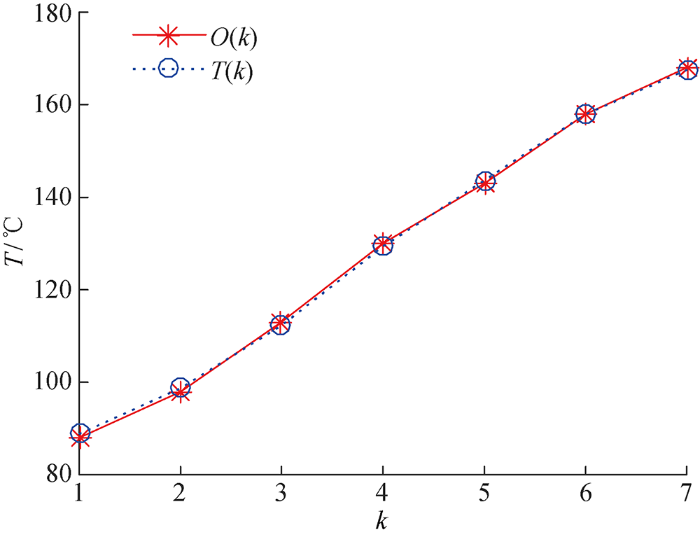
将降维后的输入向量送入ELM网络,输出为温度,隐含层节点数为20,训练ELM网络.目标涂层7组测试样本的仿真结果如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 目标涂层温度的ELM网络输出与实测值比较

Fig.8 Comparison of coating target temperature between estimated values obtained by ELM network and practical values

从图8中可以看出,网络的输出温度与样本的实际温度比较吻合.目标涂层7个测试样本的测温结果以及相对误差如表6所示.

表6 涂层的测温结果以及相对误差

Tab.6 Temperature measurement results and relative errors of coating target

T₁/℃	T₂/ ℃	$\frac{\|O (k) - T (k)\|}{O (k)}$ /%	$\bar{ε}$
88	88.8148	0.93	0.8197
98	98.7474	0.71	0.8026
113	112.3211	0.60	0.7718
130	129.3978	0.46	0.6684
143	143.6489	0.45	0.5941
158	157.9227	0.04	0.5364
168	167.5493	0.27	0.5143

新窗口打开| 下载CSV

由表6可以看出,目标涂层7个测试样本的测温结果与真实温度很相近,相对误差都不大,最大相对误差为0.93%,说明这种测温方法精度很高,进一步验证了该方法的合理性.所测材料的光谱发射率未知,沿用黑体测试的思路,根据估计的温度计算对应理想黑体的亮度值,根据式(16)就可获取材料的光谱发射率,为下一步实验验证提供数据指导和支持.由表6中给出的所测材料不同温度下测量波段的平均发射率可以看出其低发射率的特征.

4 结语

本文提出一种未知目标发射率的红外辐射测温方法.由红外辐射基本定律,目标温度与光谱辐射亮度之间存在着强非线性关系,很难应用常规辨识建模方法.建立一种基于主元分析与极限学习机相结合的测温模型.首先,建立能够充分包含温度估计信息的高维输入向量;利用PCA实现输入降维,确定线性无关的主元输入变量;利用ELM网络自适应学习多光谱亮度与目标温度之间的潜在规律,建立目标温度测温模型,最终构建未知发射率情况下的目标红外多光谱测温方法框架.用黑体和未知发射率的隐身材料涂层分别作为测试目标,获得的测温结果与实际温度的相对误差都很小,说明了这种测温方法的合理性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨永军, 王中宇, 张术坤, 等.

基于多光谱测温优化的材料光谱发射率测量

[J]. 北京航空航天大学学报, 2014, 40(8): 1022-1026.