基于Newmark隐式时间积分方案的裂纹动态扩展的数值计算方法

doi:10.16183/j.cnki.jsjtu.2020.021

基于Newmark隐式时间积分方案的裂纹动态扩展的数值计算方法

郭德平¹^,², 李铮^,³, 彭森林⁴, 曾志凯³, 吴岱峰³

1.叙镇铁路有限责任公司, 云南昭通 657900

2.武汉大学土木建筑工程学院, 武汉 430072

3.重庆市城市建设投资(集团)有限公司, 重庆 400023

4.重庆大学土木工程学院, 重庆 400045

Numerical Calculation Method for Crack Dynamic Propagation Based on Newmark Implicit Time Integration Scheme

GUO Deping¹^,², LI Zheng^,³, PENG Senlin⁴, ZENG Zhikai³, WU Daifeng³

1. Xuzhen Railway Co., Ltd., Zhaotong 657900, Yunnan, China

2. School of Civil Engineering, Wuhan University, Wuhan 430072, China

3. Chongqing City Construction Investment (Group) Co., Ltd., Chongqing 400023, China

4. Department of Civil Engineering, Chongqing University, Chongqing 400045, China

通讯作者: 李铮,男,博士;E-mail:2756232300@qq.com.

责任编辑: 陈晓燕

收稿日期: 2020-01-14

基金资助:

国家自然科学基金重点项目(51679017)
国家自然科学基金重点项目(51839009)

Received: 2020-01-14

作者简介 About authors

郭德平(1983-),男,高级工程师,主要从事隧道工程和岩土工程等方面的科研工作

摘要

扩展有限单元法(XFEM)是基于单位分解的思想,在常规有限元的位移模式中加入能够反映裂纹面不连续性的跳跃函数和裂纹尖端的渐近位移场函数,避免了常规有限单元法计算断裂问题时需要对裂纹尖端重新划分网格的不便以及繁重的计算量,并且裂纹的扩展独立于网格.标准有限元在处理时间积分时,在裂纹不断扩展的过程中整体刚度矩阵的自由度也会不断地增大,从而导致迭代计算无法进行.本文基于扩展有限单元法模拟动态裂纹扩展的方法,提出了新的Newmark隐式时间积分方案.此方法将所有节点都富集Heaviside函数和裂纹尖端的渐近位移场函数,即每个节点都有12个自由度,从而使得总体刚度矩阵式保持一致,避免迭代计算无法进行.同时,提出了一种稀疏矩阵技术来解决矩阵所占内存大和计算时间长的问题.

关键词： 扩展有限元; 动态裂纹; Newmark隐式时间积分; 稀疏矩阵技术

Abstract

Extended finite element method (XFEM) is based on the idea of unit decomposition. The jump function that can reflect the discontinuity of the crack surface and the progressive displacement field function of the crack tip is added to the conventional finite element displacement mode, which avoids the inconvenience of remeshing the crack tip and the heavy calculation. Then the conventional finite element method calculates the fracture problem, and the crack propagation is independent of the mesh. When the standard finite element deals with time integration, the degree of freedom of the overall stiffness matrix will continue to increase in the process of crack propagation, which makes iterative calculation impossible. This paper proposes a novel Newmark implicit time integration scheme based on the XFEM to simulate dynamic crack growth. This method enriches all the nodes with the Heaviside function and the asymptotic displacement field function at the crack tip, that is, each node has 12 degrees of freedom, so that the overall stiffness matrix is consistent without making iterative calculation impossible. At the same time, a sparse matrix technology is proposed to solve the problems of large memory and long calculation time occupied by the matrix.

Keywords： extended finite element method (XFEM); dynamic cracks; Newmark implicit time integration scheme; sparse matrix technique

PDF (1724KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郭德平, 李铮, 彭森林, 曾志凯, 吴岱峰. 基于Newmark隐式时间积分方案的裂纹动态扩展的数值计算方法[J]. 上海交通大学学报（自然版）, 2021, 55(6): 689-697 doi:10.16183/j.cnki.jsjtu.2020.021

GUO Deping, LI Zheng, PENG Senlin, ZENG Zhikai, WU Daifeng. Numerical Calculation Method for Crack Dynamic Propagation Based on Newmark Implicit Time Integration Scheme[J]. Journal of shanghai Jiaotong University, 2021, 55(6): 689-697 doi:10.16183/j.cnki.jsjtu.2020.021

随着21世纪我国基础设施大规模建设的进行,西部大开发战略的实施以及世界经济危机以来国家对基础设施建设的投资,我国的铁路、公路、大中型水电站建设以及南水北调、西气东输等工程将有大量的长大隧道需要建设.因此,隧道掘进机(TBM)在我国的应用前景非常广阔,我国对掘进机及其技术的需求猛增.

在工程建设和运营过程中,结构或者裂隙岩体会受到多种形式的动力作用(如爆破、地震等),在动荷载的作用下更容产生失稳破坏,故针对裂纹动态扩展的研究引起了广泛的关注^[1,2,3].Sun等^[4]基于有限元方法比较了显式时间积分和隐式时间积分在分析线性和非线性动力问题中的区别.2012年,Nilsson等^[5]在黏结单元中嵌入裂纹,分析了动荷载作用于弹塑性厚板的动力响应.

扩展有限单元法(XFEM)^[6,7,8,9]是近十五年发展起来的一种在常规有限元框架内求解不连续问题,特别是裂纹扩展问题的数值方法.其原理是在裂纹影响区域的单元结点上用裂尖渐近位移场函数及跳跃函数加强传统有限元的基,以考虑由于裂纹存在引起的位移不连续性,继承了标准有限元的所有优点,但其所使用的网格与结构内部的几何和物理界面无关,从而避免了常规有限元方法中的网格重构,不需要裂纹面与有限元网格一致,不需要在裂缝周围布置高密度网格,大大简化了裂纹扩展的分析过程.能够很容易刻画出裂纹面上位移的强不连续性质和裂纹尖端的应力奇异性,并且无需重新划分网格.2001年,Stolarska等^[10]将水平集函数引入XFEM来描述裂纹的位置和裂纹扩展之后的更新位置.裂纹的几何位置能够很容易用两个零水平集函数来表达,这两个零水平集函数在裂纹尖端处彼此正交.同时,随着裂纹的扩展,裂纹面和裂纹尖端处需要富集的节点能够实时更新.

Zhou等^[11]在推导扩展有限元算法的基础上,分析了应力强度因子的J积分计算方法及积分区域的选取.基于扩展有限元法对I型裂纹进行了计算,有限元网格独立于裂纹面,无需在裂纹尖端加密网格.Chen等^[12]引入裂纹交叉汇合加强函数以分析多裂纹交叉汇合过程,并且在裂纹附近区域使用广义形函数,并引入线增函数消除混合单元,可有效提高裂纹附近的精度.黄宏伟等^[13]在这些研究的基础上,采用扩展有限元研究了衬砌在主要影响因素作用下的裂缝分布规律、裂缝扩展过程、裂缝外观表现形式及发生机制.阮滨等^[14]基于扩展有限元法对均质土坝坝顶的初始裂纹扩展路径进行了模拟,研究结果表明扩展有限元法对网格划分的要求比较高,网格须均匀,网格的疏密程度对计算的结果影响不大.Menouillard等^[15]提出利用无网格近似方法的XFEM富集方案,该方法采用显式时间积分方案来分析动力过程.Wen等^[16]基于改进的扩展有限单元法研究了裂纹动态扩展问题的计算精度和算法稳定性问题.

但是标准有限元在处理时间积分时,在裂纹不断扩展的过程中整体刚度矩阵的自由度也会不断的增大,从而导致迭代计算无法进行.本文基于扩展有限单元法模拟动态裂纹扩展的方法,提出了新的时间积分方案.将所有节点都富集Heaviside函数和裂纹尖端的渐近位移场函数,即每个节点都有12个自由度,从而使得总体刚度矩阵式保持一致,避免迭代计算式无法进行的情况.提出了一种稀疏矩阵技术来解决矩阵所占内存大和计算时间长的问题.

1 动力扩展有限元的控制方程

1.1 控制方程的强形式

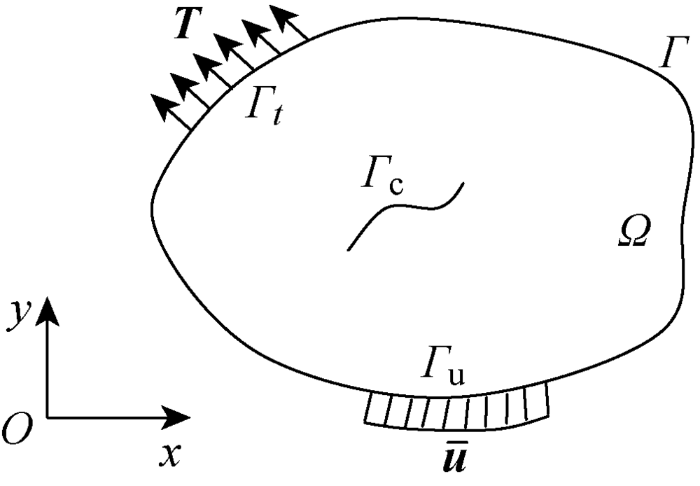
如图1所示,在绝对坐标系xOy中,区域Ω的边界为Γ, $Γ_{t}$ (t为时间)为与时间有关的瞬时边界, $Γ_{c}$ 为裂纹附近边界, $Γ_{u}$ 为位移边界,作用在 $Γ_{t}$ 的边界面力记为T,作用在整个区域Ω内的体力记为f,位移边界记为 $\bar{u}$ .值得注意的是,边界面力T和体力f都是动荷载. $Γ = Γ_{u} ⋃ Γ_{t} ⋃ Γ_{c} .$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 在动荷载作用下含有裂纹的二维区域示意图

Fig.1 Diagram of two-dimensional domain containing a crack subjected to dynamic loads

动力平衡方程的强形式为

(1)

\begin{matrix} Δ \cdot σ + f - μ \overset{\cdot}{U} - ρ \ddot{U} = 0, 在 Ω 内 \end{matrix}

式中:σ为柯西应力张量;μ为材料的阻力系数;ρ为材料的密度;U为位移场, $\overset{\cdot}{U}$ 和 $\ddot{U}$ 分别为速度场和加速度场,并且 $\overset{\cdot}{U} = d U / d t$ 和 $\ddot{U} = \overset{\cdot}{d U} / d t$ .

该二维区域的应力边界条件和位移边界条件为

(2)

σ \cdot n_{t} = T, 在 Γ_{t} 上

(3)

σ \cdot n_{c} = 0, 在 Γ_{c} 上

(4)

U \cdot n_{u} = 0, 在 Γ_{u} 上

式中:n_t为边界Γ_t的单位外法向量;n_c为边界Γ_c的单位外法向量;n_u为边界Γ_u的单位外法向量.

在小应变和小位移的条件下,几何方程可以表达为

(5)

ε = ▽_{s} U = \frac{1}{2} (▽ U + ▽ U^{T})

式中:ε为应变张量;▽_s为梯度算子的对称部分.

根据广义胡克定律,σ与应变张量的之间的关系可以表达为

(6)

σ = C ∶ ε

式中:C为Hooke张量.

1.2 控制方程的等效弱形式

根据虚位移原理,引入虚位移δU,式(1)可以改写为

(7)

\begin{array}{l} \int_{Ω} (Δ σ + f) \cdot δ U d V - \int_{Ω} μ \overset{\cdot}{U} \cdot δ U d V - \\ \int_{Ω} ρ \ddot{U} \cdot δ U d V - \int_{Γ_{t}} (σ \cdot n_{t} - T) \cdot δ U d Γ = 0 \end{array}

再根据分部积分,式(7)可以化简为

(8)

\begin{array}{l} \int_{Ω} (- σ \cdot δ ε + f \cdot δ U) d V - \int_{Ω} μ \overset{\cdot}{U} \cdot δ U d V - \\ \int_{Ω} ρ \ddot{U} \cdot δ U d V + \int_{Γ_{t}} T \cdot δ U d Γ = 0 \end{array}

由变分原理将式(8)的第一项进行变换为

(9)

σ \cdot δ ε = δ (\frac{1}{2} ε^{T} ∶ C ∶ ε)

因此,该二维区域的能量系统的泛函数可以用下式表达

(10)

\begin{array}{l} Π = \int_{Ω} \frac{1}{2} ε^{T} ∶ C ∶ ε d V - \int_{Ω} U^{T} \cdot f d V + \\ \int_{Ω} U^{T} \cdot μ \overset{\cdot}{U} d V + \int_{Ω} U^{T} \cdot ρ \ddot{U} d V - \int_{Γ_{t}} U^{T} \cdot T d Γ \end{array}

对式(10)进行变分,并结合式(8)可以得到:

(11)

\begin{array}{l} δΠ = \frac{\partial Π}{\partial U} δU = \\ \int_{Ω} (σ \cdot δε - f \cdot δ U) d V + \int_{Ω} μ \overset{\cdot}{U} \cdot δ U d V + \\ \int_{Ω} ρ \ddot{U} \cdot δ U d V - \int_{Γ_{t}} T \cdot δ U d Γ = 0 \end{array}

因此有,

(12)

\begin{matrix} \frac{\partial Π}{\partial U} = 0 \end{matrix}

1.3 区域的空间离散

水平集法是裂纹和非连续面追踪强有力的工具.Zhou等^[17]首次引入水平集法来研究材料内部界面的追踪定位和形状描述.如图2所示,一根裂纹可以用2个在裂纹尖端彼此相互正交的零水平集函数 $ϕ (x)$ 和 $ψ (x)$ 表示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

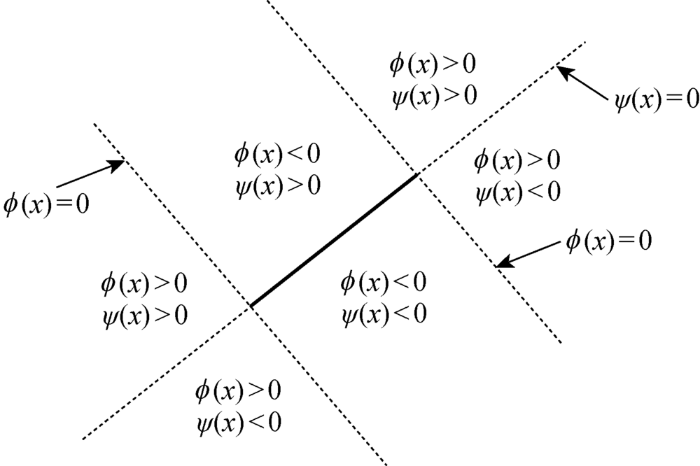
图2 用于追踪裂纹的两个零水平集函数原理图

Fig.2 Schematic diagram of two zero-level set functions used to track cracks

Stolarska等^[10]给出了水平集法的更新算法,水平集函数 $ϕ (x)$ 的更新算法为

(13)

ϕ_{i + 1} (x) = ϕ_{i} (x) - Δ t (u_{i} \frac{\partial ϕ_{i} (x)}{\partial x} + v_{i} \frac{\partial ϕ_{i} (x)}{\partial y})

式中: $ϕ_{i + 1} (x)$ 为水平集函数ϕ(x)的更新值;Δt为时间增量; $u_{i}$ 和 $v_{i}$ 分别为裂纹尖端沿x和y方向扩展的速度.

对于水平集函数 $ψ (x),$ 其更新算法为

(14)

\begin{array}{l} ψ_{i + 1} (x) = \\ \{\begin{array}{l} ψ_{i} (x) \\ \pm |(x - x_{i}) \frac{F_{y}}{‖ F ‖} - (y - y_{i}) \frac{F_{x}}{‖ F ‖}| \end{array} \end{array}

式中: $F = [F_{x} F_{y}]$ 为裂纹尖端在裂纹面外法线方向的速度矢量; $(x_{i}, y_{i})$ 为裂纹尖端的坐标.

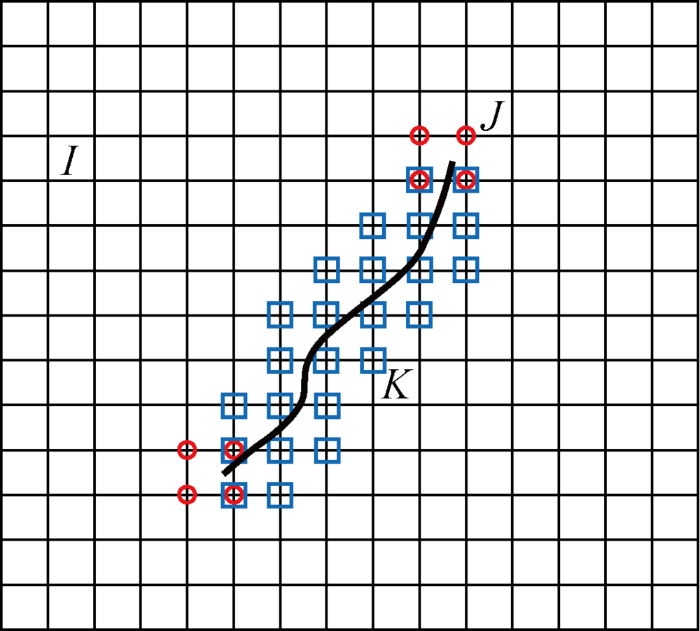
如图3所示,区域Ω被离散化成 $n^{e}$ 个单元,I表示该区域所有节点,J表示裂纹面上被Heaviside函数富集的节点集合,由蓝色正方形标识,K表示裂纹尖端上被渐近位移场函数富集的节点集合,由红色圆圈形标识.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 扩展有限单元法的节点富集方案

Fig.3 Enrichment scheme of XFEM

根据文献[6,18]的研究,单元位移场可以表达为

(15)

\begin{array}{l} U^{e} (x) = \sum_{I} N (x) U_{a}^{e} + \sum_{J} H_{Γ_{c}} N (x) U_{b}^{e} + \\ \sum_{K} N_{φ} (x) U_{c}^{e} \end{array}

式中:U^e(x)为单元位移场矩阵;N为常规有限元的形函数矩阵; $U_{a}^{e}$ 为常规节点的单元自由度位移值矩阵; $H_{Γ_{c}}$ 为Heaviside函数,有 $H_{Γ_{c}} (x) = \{\begin{array}{l} + 1, & ψ (x) > 0 \\ - 1, & ψ (x) < 0 \end{array}; U_{b}^{e}$ 为Heaviside函数富集节点的单元自由度位移值矩阵; $U_{c}^{e}$ 为裂纹尖端富集节点的单元自由度位移值矩阵;N_φ(x)为裂纹尖端富集后的形函数.

对于四边形单元,上述3种自由度位移值矩阵 $U_{a}^{e}$ 、 $U_{b}^{e}$ 及 $U_{c}^{e}$ 展开为

(16)

U_{a}^{e} = {[\begin{array}{l} a_{1 x} & a_{1 y} & \dots & a_{4 x} & a_{4 y} \end{array}]}^{T}

(17)

U_{b}^{e} = {[\begin{array}{l} b_{1 x} & b_{1 y} & \dots & b_{4 x} & b_{4 y} \end{array}]}^{T}

(18)

U_{c}^{e} = [c_{1 x 1} c_{1 y 1} c_{1 x 2} c_{1 y 2} c_{1 x 3} c_{1 y 3} c_{1 x 4} c_{1 y 4} \dots c_{4 x 1} c_{4 y 1} c_{4 x 2} c_{4 y 2} c_{4 x 3} c_{4 y 3} c_{4 x 4} c_{4 y 4}]^{T}

式中: $a_{ix}$ 和 $a_{iy}$ 分别为第i个节点在x和y方向的自由度位移值; $b_{ix}$ 和 $b_{iy}$ 分别为第i个Heaviside函数富集节点在x和y方向的附加自由度位移值; $c_{ixj}$ 和 $c_{iyj}$ 分别为第i个节点的第j个附加自由度沿x和y方向的附加自由度位移值.

根据Wu等^[19]的研究,线弹性材料中的I型、II 型及 III 型裂纹尖端渐近位移场均可由几个特定的基函数组成的函数形式来表达,为了能体现出裂纹尖端渐近位移场的奇异性,将该组基函数引入裂纹尖端的位移场计算,如下:

(19)

φ_{i} (x) = [\sqrt[]{r} \sin \frac{θ}{2} \sqrt[]{r} \cos \frac{θ}{2} \sqrt[]{r} \sin \frac{θ}{2} \sin θ \sqrt[]{r} \cos \frac{θ}{2} \sin θ]

(20)

r = \sqrt[]{(x - x_{tip})^{2} + (y - y_{tip})^{2}}

(21)

θ = \arctan \frac{y - y_{tip}}{x - x_{tip}} - α

式中:(r,θ)是以裂纹尖端为原点建立的极坐标系的坐标值; $(x_{tip}, y_{tip})$ 是绝对坐标系中裂纹尖端的坐标值,坐标系的建立如图4所示,x'O'y'为以裂纹尖端建立的局部坐标系, 其中α为裂纹中心线与绝对坐标系x轴的夹角.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 裂纹面上的两套坐标系

Fig.4 Two coordinate systems of crack surface

裂纹尖端富集后的形函数N_φ(x)可以表达为

(22)

N_{φ} = [\begin{array}{l} N_{φ, 11} & N_{φ, 12} & N_{φ, 13} & N_{φ, 14} \\ N_{φ, 41} & N_{φ, 42} & N_{φ, 43} & N_{φ, 44} \end{array}]

式中: $N_{φ, ij} = [\begin{array}{l} N_{i} φ_{j} & 0 \\ 0 & N_{i} φ_{j} \end{array}] (1 \leq i, j \leq 4) .$

φ_j为尖端位移场.将式(15)代入式(5),可以得到单元的应变张量ε^e(x)如下:

(23)

\begin{array}{l} ε^{e} (x) = Δ_{s} U^{e} (x) = \\ AN (x) U_{a}^{e} + H_{Γ_{c}} AN (x) U_{b}^{e} + A N_{φ} (x) U_{c}^{e} = \\ B_{a} (x) U_{a}^{e} + B_{b} (x) U_{b}^{e} + B_{c} (x) U_{c}^{e} \end{array}

式中:微分算子 $A = [\begin{array}{l} \frac{\partial}{\partial x} & 0 \\ 0 & \frac{\partial}{\partial y} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial x} \end{array}]$ ; $B_{a} (x) = [\begin{array}{l} N_{i, x} (x) & 0 \\ 0 & N_{i, y} (x) \\ N_{i, y} (x) & N_{i, x} (x) \end{array}]$ ,(i=1, 2, 3, 4);B_b(x)= $H_{Γ_{c}}$ B_a(x);B_c(x)= $[\begin{array}{l} \frac{\partial}{\partial x} & 0 \\ 0 & \frac{\partial}{\partial y} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial x} \end{array}]$ N_φ.

再将式(15)、(23)代入式(10)中可以得到:

(24)

\begin{array}{l} Π = \sum_{e} Π^{e} = \sum_{e} (U^{eT} \int_{Ω^{e}} \frac{1}{2} {\tilde{B}}^{T} D \tilde{B} d v U^{e}) - \\ \sum_{e} (U^{eT} \int_{Ω^{e}} {\tilde{N}}^{T} fd v) + \sum_{e} (U^{eT} \int_{Ω^{e}} μ {\tilde{N}}^{T} \tilde{N} d v {\ddot{U}}^{e}) + \\ \sum_{e} (U^{eT} \int_{Ω^{e}} ρ {\tilde{N}}^{T} \tilde{N} d v {\overset{\cdot}{U}}^{e}) - \sum_{e} (U^{eT} \int_{Γ_{t}} {\tilde{N}}^{T} T d Γ) \end{array}

式中:Π^e为单元泛函数;Ω^e为单元区域; $\tilde{B}$ 为广义的应变矩阵,其包含B_a(x),B_b(x)及B_c(x); $\tilde{N}$ 为广义形函数,其包含N(x), $H_{Γ_{c}}$ N(x)及N_φ(x).

将式(24)代入式(11)并化简,可以得到:

(25)$\begin{matrix} & \text{ }\!\!\delta\!\!\text{ }\!\!\Pi\!\!\text{ }=\delta {{U}_{\text{a}}}({{M}_{\text{aa}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{a}}}+{{M}_{\text{ab}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{b}}}+{{M}_{\text{ac}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{c}}}+{{C}_{\text{aa}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{a}}} \\ & +{{C}_{\text{ab}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{b}}}+{{C}_{\text{ac}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{c}}}+{{K}_{\text{aa}}}{{U}_{\text{a}}}+{{K}_{\text{ab}}}{{U}_{\text{b}}}+{{K}_{\text{ac}}}{{U}_{\text{c}}}-{{P}_{\text{a}}}) \\ & +\text{ }\!\!\delta\!\!\text{ }{{U}_{\text{b}}}({{M}_{\text{ba}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{a}}}+{{M}_{\text{bb}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{b}}}+{{M}_{\text{bc}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{c}}}+{{C}_{\text{ba}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{a}}}+{{C}_{\text{bb}}} \\ & {{\overset{\cdot }{\mathop{U}}\,}_{\text{b}}}+{{C}_{\text{bc}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{c}}}+{{K}_{\text{ba}}}{{U}_{\text{a}}}+{{K}_{\text{bb}}}{{U}_{\text{b}}}+{{K}_{\text{bc}}}{{U}_{\text{c}}}-{{P}_{\text{b}}})+\text{ }\!\!\delta\!\!\text{ }{{U}_{\text{c}}} \\ & ({{M}_{\text{ca}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{a}}}+{{M}_{\text{cb}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{b}}}+{{M}_{\text{cc}}}{{\overset{\ddot{\ }}{\mathop{\text{U}}}\,}_{\text{c}}}+{{C}_{\text{ca}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{a}}}+{{C}_{\text{cb}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{b}}}+ \\ & {{C}_{\text{cc}}}{{\overset{\cdot }{\mathop{U}}\,}_{\text{c}}}+{{K}_{\text{ca}}}{{U}_{\text{a}}}+{{K}_{\text{cb}}}{{U}_{\text{b}}}+{{K}_{\text{cc}}}{{U}_{\text{c}}}-{{P}_{\text{c}}}) \\ \end{matrix}$

式中:

$\begin{array}{l} M_{aa} = \sum_{e} \int_{Ω^{e}} ρ N^{T} N d v \\ M_{ab} = M_{ba}^{T} = \sum_{e} \int_{Ω^{e}} ρ H_{Γ_{c}} N^{T} N d v \\ M_{ac} = M_{ac}^{T} = \sum_{e} \int_{Ω^{e}} ρ N^{T} N_{φ} d v \\ C_{aa} = \sum_{e} \int_{Ω^{e}} μ N^{T} N d v \\ C_{ab} = C_{ba}^{T} = \sum_{e} \int_{Ω^{e}} μ H_{Γ_{c}} N^{T} N d v \\ C_{ac} = C_{ac}^{T} = \sum_{e} \int_{Ω^{e}} μ N^{T} N_{φ} d v \\ K_{aa} = \sum_{e} \int_{Ω^{e}} B_{a}^{T} D B_{a} dv \\ K_{ab} = K_{ba}^{T} = \sum_{e} \int_{Ω^{e}} B_{a}^{T} D B_{b} dv \\ K_{ac} = K_{ca}^{T} = \sum_{e} \int_{Ω^{e}} B_{a}^{T} D B_{c} dv \\ P_{a} = \sum_{e} (\int_{Ω^{e}} N^{T} f d v + \int_{Γ_{c}^{e}} N^{T} T d v) \\ P_{b} = \sum_{e} (\int_{Ω^{e}} H_{Γ_{c}} N^{T} f d v + \int_{Γ_{c}^{e}} H_{Γ_{c}} N^{T} T d v) \\ P_{c} = \sum_{e} (\int_{Ω^{e}} N_{φ}^{T} f d v + \int_{Γ_{c}^{e}} N_{φ}^{T} T d v) \end{array}$

考虑到3种类型的自由度位移值U_a、U_b及U_c式彼此相互独立的,结合变分原理,将式(25)代入式(12),可以得到:

(26)

\begin{array}{l} [\begin{array}{l} M_{aa} & M_{ab} & M_{ac} \\ M_{ba} & M_{bb} & M_{bc} \\ M_{ca} & M_{cb} & M_{cc} \end{array}] [\begin{array}{l} {\ddot{U}}_{a} \\ {\ddot{U}}_{b} \\ {\ddot{U}}_{c} \end{array}] + [\begin{array}{l} C_{aa} & C_{ab} & C_{ac} \\ C_{ba} & C_{bb} & C_{bc} \\ C_{ca} & C_{cb} & C_{cc} \end{array}] [\begin{array}{l} {\overset{\cdot}{U}}_{a} \\ {\overset{\cdot}{U}}_{b} \\ {\overset{\cdot}{U}}_{c} \end{array}] + \\ [\begin{array}{l} K_{aa} & K_{ab} & K_{ac} \\ K_{ba} & K_{bb} & K_{bc} \\ K_{ca} & K_{cb} & K_{cc} \end{array}] [\begin{array}{l} U_{a} \\ U_{b} \\ U_{c} \end{array}] = [\begin{array}{l} P_{a} \\ P_{b} \\ P_{c} \end{array}] \end{array}

根据式(26),扩展有限单元法的运动学方程为

(27)

\begin{matrix} M^{t} {\ddot{U}}^{t} + C^{t} {\overset{\cdot}{U}}^{t} + K^{t} U^{t} = P^{t} \end{matrix}

式中:M^t为质量矩阵;C^t为阻力矩阵;K^t为刚度矩阵;P^t为等效节点载荷向量;U^t、 ${\overset{\cdot}{U}}^{t}$ 及 ${\ddot{U}}^{t}$ 分别为t时刻位移场、速度场及加速度场的向量.

1.4 时间积分方案

在扩展有限单元法的计算中,时间积分会遇到困难.时间积分基于迭代的算法,而在裂纹不断扩展的过程中整体刚度矩阵的自由度也会不断的增大,从而导致迭代计算无法进行.在每次迭代中,时间积分会涉及当前步的位移场U^t和下一步的位移场U^t^+Δ^t,具体表达式为

(28)

\begin{matrix} {\ddot{U}}^{t} = \frac{1}{Δ t^{2}} (U^{t - Δ t} - 2 U^{t} + U^{t + Δ t}) \end{matrix}

(29)

{\overset{\cdot}{U}}^{t} = \frac{1}{2 Δ t} (- U^{t - Δ t} + U^{t + Δ t})

本文提出的时间积分方案是将所有节点都富集Heaviside函数和裂纹尖端的渐近位移场函数,即每个节点都有12个自由度,从而使得总体刚度矩阵式保持一致,而避免迭代计算式无法进行.但是,将所有节点都富集Heaviside函数和裂纹尖端的渐近位移场函数的代价是刚度矩阵的阶数增多,从而使得参与运算的矩阵所占内存和计算时间急剧增加.为此,本文提出了一种稀疏矩阵技术来解决矩阵所占内存大和计算时间长的问题.

对于两个常规有限元的自由度,若该节点的某个方向被约束(约束状态),那么所对应的自由度值被定义为0,若该节点的某个方向没有被约束(激活状态),那么所对应的自由度值作为未知数参与计算.对于两个Heaviside函数富集的自由度,若该节点不属于集合J时(约束状态),这两个自由度位移值被定义为0,若该节点属于集合J时(激活状态),这两个自由度位移值作为未知数参与计算.对于另外8个裂纹尖端渐近位移场函数富集的自由度,若该节点不属于集合K时(约束状态),这8个自由度位移值被定义为0,若该节点属于集合K时(激活状态),这8个自由度位移值作为未知数参与计算.

根据上述定义,可以得到一个将每个节点有两个自由度的体系(简称二维体系)映射到每个节点有12个自由度的体系(简称十二维体系)中的转换矩阵,该转换矩阵的构造方法如下:

(30)

\begin{matrix} L^{t} = [\begin{array}{l} L_{11} & L_{12} & \dots & L_{1 j} & \dots & L_{1 m} \\ L_{21} & L_{22} & \dots & L_{2 j} & \dots & L_{2 m} \\ ︙ & ︙ & ⋱ & ︙ & ⋱ & ︙ \\ L_{i 1} & L_{i 2} & \dots & 1 & \dots & L_{im} \\ ︙ & ︙ & ⋱ & ︙ & ⋱ & ︙ \\ L_{n 1} & L_{n 2} & \dots & L_{nj} & \dots & L_{nm} \end{array}] \end{matrix}

式中:变量n和m根据模型的节点个数来定.二维体系中的第i个自由度映射于12维体系中的第j个自由度,当该自由度是激活状态时,该矩阵中所有元素为1,当该自由度是约束状态时,该矩阵中所有元素为0.

那么,12维体系中的质量矩阵 ${\tilde{M}}^{t}$ 、阻尼矩阵 ${\tilde{C}}^{t}$ 、刚度矩阵 ${\tilde{K}}^{t}$ 及等效节点载荷向量 ${\tilde{P}}^{t}$ 可以分别表示为

(31)

{\tilde{M}}^{t} = (L^{t})^{T} M^{t} L^{t} + I_{m \times m}^{t} - (L^{t})^{T} L^{t}

(32)

{\tilde{C}}^{t} = (L^{t})^{T} C^{t} L^{t} + I_{m \times m}^{t} - (L^{t})^{T} L^{t}

(33)

{\tilde{K}}^{t} = {(L)}^{T} K^{t} L^{t} + I_{m \times m}^{t} - {(L)}^{T} L^{t}

(34)

{\tilde{P}}^{t} = (L^{t})^{T} P^{t}

式中: $I_{m \times m}^{t}$ 是与时间有关的m阶单位矩阵.

那么,扩展有限单元法在12维体系中的运动方程为

(35)

\begin{matrix} {\tilde{M}}^{t} {\tilde{\ddot{U}}}^{t} + {\tilde{C}}^{t} {\tilde{\overset{\cdot}{U}}}^{t} + {\tilde{K}}^{t} {\tilde{U}}^{t} = {\tilde{P}}^{t} \end{matrix}

对于时间积分,本文采用Newmark隐式时间积分方案如下:

(36)${{\tilde{\dot{U}}}^{t+\Delta t}}={{\tilde{\dot{U}}}^{\text{t}}}+[(1-\xi ){{\tilde{\ddot{U}}}^{t}}+\xi {{\tilde{\ddot{U}}}^{t+\Delta t}}]\Delta t$

(37)${{\tilde{U}}^{t+\Delta t}}={{\tilde{U}}^{t}}+{{\tilde{\dot{U}}}^{\text{t}}}\Delta t+[(\frac{1}{2}-\eta ){{\tilde{\ddot{U}}}^{t}}+\eta {{\tilde{\ddot{U}}}^{t+\Delta t}}]\Delta {{t}^{2}}$

式中:ξ和η分别为Newmark隐式时间积分方案中的参数.

在Newmark隐式时间积分方案中, $t + Δ t$ 时刻的位移场为

(38)

{\tilde{M}}^{t + Δ t} {\tilde{\ddot{U}}}^{t + Δ t} + {\tilde{C}}^{t + Δ t} {\tilde{\overset{\cdot}{U}}}^{t + Δ t} + {\tilde{K}}^{t + Δ t} {\tilde{U}}^{t + Δ t} = {\tilde{P}}^{t + Δ t}

联合式(36)~(38),可以得到12维体系的位移场的求解方程式:

(39)

\begin{matrix} {\overset{⌒}{K}}^{t + Δ t} {\tilde{U}}^{t + Δ t} = {\overset{⌒}{P}}^{t + Δ t} \end{matrix}

式中:$\begin{matrix} & {{{\overset{\scriptscriptstyle\frown}{K}}}^{\text{t}+\Delta \text{t}}}={{{\tilde{K}}}^{\text{t}+\Delta \text{t}}}+\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }{{t}^{2}}}{{{\tilde{M}}}^{\text{t}+\Delta \text{t}}}+\frac{\xi }{\eta \text{ }\!\!\Delta\!\!\text{ }t}{{{\tilde{C}}}^{\text{t}+\Delta \text{t}}}, \\ & {{{\overset{\scriptscriptstyle\frown}{P}}}^{\text{t}+\Delta \text{t}}}={{{\tilde{P}}}^{\text{t}+\Delta \text{t}}}+{{{\tilde{M}}}^{\text{t}+\Delta \text{t}}}\left[ \frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }{{t}^{2}}}{{{\tilde{U}}}^{t}}+\frac{1}{\eta \text{ }\!\!\Delta\!\!\text{ }t}{{{\tilde{\dot{U}}}}^{t}}+\left( \frac{1}{2\eta }-1 \right){{{\tilde{\ddot{U}}}}^{t}} \right]+ \\ & {{{\tilde{C}}}^{\text{t}+\Delta \text{t}}}\left[ \frac{\xi }{\eta \text{ }\!\!\Delta\!\!\text{ }t}{{{\tilde{U}}}^{t}}+\left( \frac{\xi }{\eta }-1 \right){{{\tilde{\dot{U}}}}^{t}}+\left( \frac{\xi }{2\eta }-1 \right){{{\tilde{\ddot{U}}}}^{t}} \right]. \\ \end{matrix}$

该方程的初始条件是:

(40)

{\tilde{U}}^{0} = 0

(41)

{\tilde{\overset{\cdot}{U}}}^{0} = 0

(42)

{\tilde{\ddot{U}}}^{0} = ({\tilde{M}}^{0})^{- 1} P^{0}

在12维体系中, $t + Δ t$ 时刻的加速度场和速度场为

(43)

{\tilde{\ddot{U}}}^{t + Δ t} = \frac{1}{η Δ t^{2}} ({\tilde{U}}^{t + Δ t} - {\tilde{U}}^{t}) - \frac{1}{η Δ t} {\tilde{\overset{\cdot}{U}}}^{t} - (\frac{1}{2 η} - 1) {\tilde{\ddot{U}}}^{t}

(44)

{\tilde{\overset{\cdot}{U}}}^{t + Δ t} = {\tilde{\overset{\cdot}{U}}}^{t} + Δ t (1 - ξ) {\tilde{\ddot{U}}}^{t} + ξ Δ t {\tilde{\ddot{U}}}^{t + Δ t}

根据Newmark时间积分方法,式(39)求解稳定的条件是ξ和η应满足^[20]:

(45)

\begin{matrix} ξ \geq 0.5, η \geq 0.25 {(0.5 + ξ)}^{2} \end{matrix}

2 实例与分析

2.1 实例1

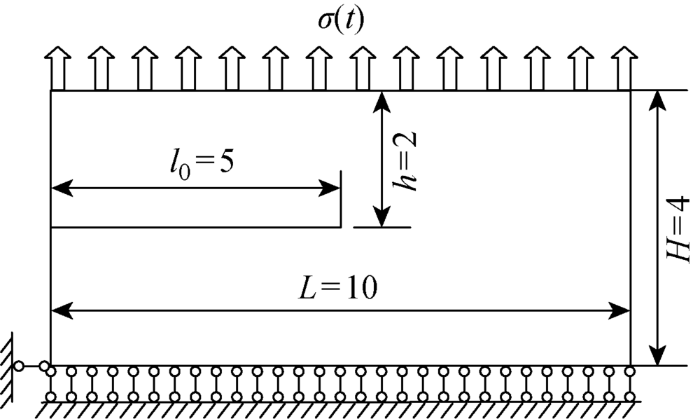
如图5所示,平面板的长L=10 m,高H=10 m.预制裂纹在板的左侧中部,其长度l₀=5 m,距离上边界高度h=2 m.板的下边界竖向被约束,左下角被水平方向约束.板的材料属性为:弹性模量E=210 GPa,泊松比ν=0.3,密度ρ=8000 kg/m³,阻尼系数μ=0.05.上边界受到动荷载σ(t)的作用,作用力的函数表达式为

(46)

σ (t) = σ_{0} f_{0} (t)

式中:等效载荷 $σ_{0} = 5 \times 10^{5} Pa$ ;与时间有关的动态表达式 $f_{0} (t) = \{\begin{array}{l} 0, & t \leq 0 \\ 1, & t > 0 \end{array} .$

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 实例1的几何布置和荷载条件(m)

Fig.5 Geometric layout and load conditions of example 1 (m)

应力波达到裂纹尖端所用的时间τ_c= ${\frac{H}{c_{d}}}^{[21]}$ ,膨胀波波速c_d=5944 m/s,那么τ_c=363.5 μs.

根据Wang等^[22,23]的研究,裂纹尖端的应力强度因子K_I的解析解为

(47)

K_{I}^{0} (\overset{\cdot}{l}, t) = K_{I}^{0} (0, t) k (\overset{\cdot}{l})

(48)

K_{I}^{0} (0, t) = \{\begin{array}{l} 0, & t < τ_{c} \\ \frac{2 σ_{0}}{1 - ν} \sqrt[]{\frac{c_{d} (t - τ_{c}) (1 - 2 ν)}{π}}, & τ_{c} \leq t \leq 3 τ_{c} \end{array}

(48)

k (\overset{\cdot}{l}) = \frac{1 - \frac{\overset{\cdot}{l}}{c_{r}}}{\sqrt[]{1 - \frac{\overset{\cdot}{l}}{c_{d}}}}

式中: $K_{I}^{0} (0, t)$ 是当裂纹扩展速度 $\overset{\cdot}{l} = 0$ 的应力强度因子;瑞丽波波速 $c_{r} = 2947 m / s.$

采用本文提出的方法计算不同时刻裂纹尖端的动态应力强度因子,再将其归一化.采用了3种不同的时间步Δt=10 μs,Δt=20 μs及Δt=50 μs,所得数值结果如图6所示.裂纹尖端动态应力强度因子在时间t=0~τ_c内几乎为0,因为这段时间应力波还没有到达裂纹的尖端.当t>τ_c时,裂纹尖端的动态应力强度因子开始逐渐增大.从如图6可以看出,本方法计算的结果与解析解的结果吻合.本方法计算的的动态应力强度因子具有一定的震荡性,但是震荡性较小,如图7所示(K_I,S为震荡值),并且震荡性随着时间的增长而逐渐衰弱.本方法计算的x方向应力σ_x的分布如图8所示,在裂纹尖端的应力集中比较明显.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 K_I的历时曲线图

Fig.6 Time history of K_I

图7

新窗口打开| 下载原图ZIP| 生成PPT

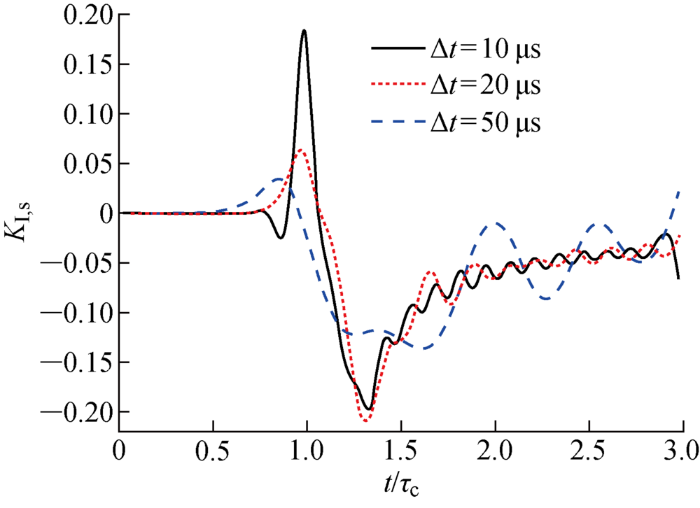
图7 不同时间步K_I的震荡历时曲线图

Fig.7 Time history of oscillation of K_I at different time steps

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 σ_x分布云图(Δt=10 μs,t=3τ_c)

Fig.8 Contour of σ_x (Δt=10 μs,t=3τ_c)

2.2 实例2

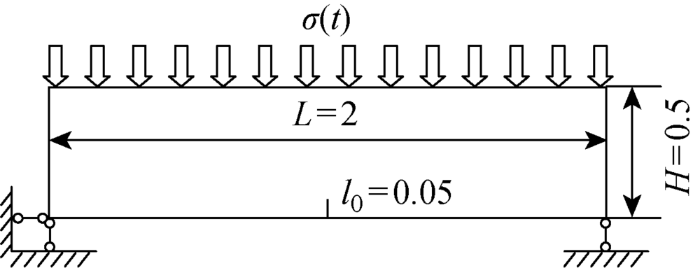
如图9所示,简支梁的长L=2 m,高H=0.5 m.预制裂纹在简支梁的下边界中部,长度l₀=0.05 m.板的下边界竖向被约束,左下角被水平方向约束,板的材料属性为:弹性模量E=210 GPa,泊松比ν=0.3,密度ρ=8000 kg/m³,阻尼系数μ=0.05,材料的断裂韧度K_IC=5×10⁵Pa· $m^{\frac{1}{2}}$ .上边界受到动荷载σ(t)的作用,作用力的函数表达式为

(50)

\begin{matrix} σ (t) = σ_{0} f_{0} (t) \end{matrix}

式中: $σ_{0} = 1.0 \times 10^{7}, f_{0} (t) = \{\begin{array}{l} 0, & t \leq 0 \\ 1, & t > 0 \end{array} .$

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 实例2的几何布置和荷载条件(m)

Fig.9 Geometric layout and load conditions of example 2 (m)

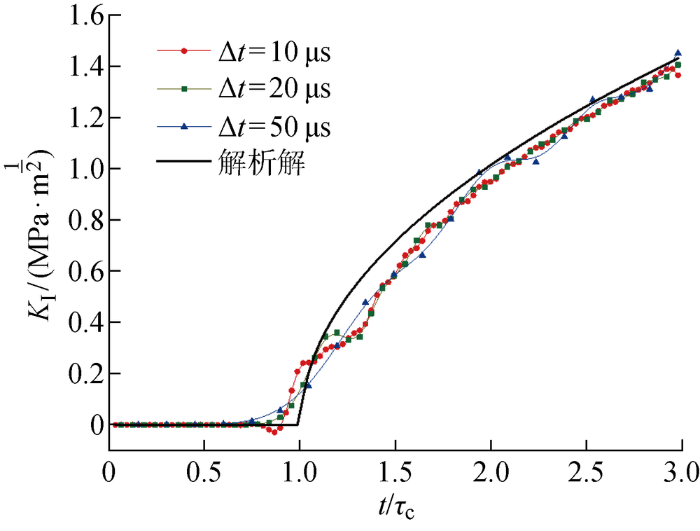
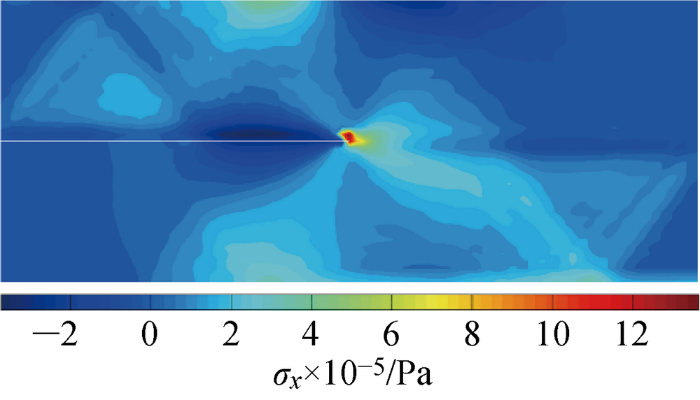
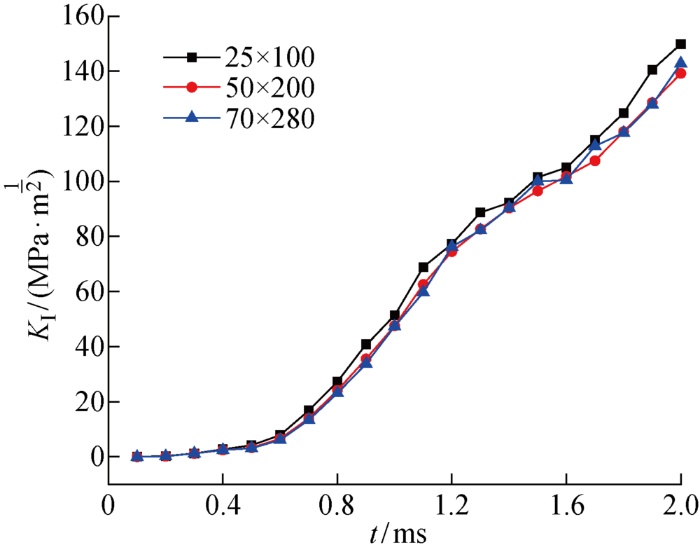
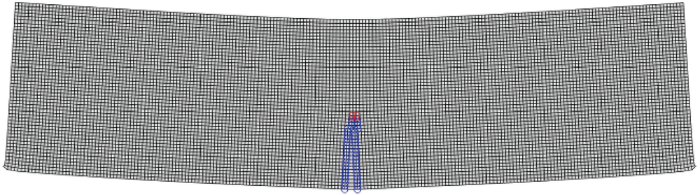
在本实例中,研究了25×100,50×200和70×280共3种不同的网格密度(行数×列数).不同网格密度下裂纹动态应力强度因子的历时曲线如图10所示,网格密度为25×100和50×200的裂纹动态应力强度因子的相关系数为 0.9993,网格密度为50×200和70×280的裂纹动态应力强度因子的相关系数为 0.9994,网格密度为25×100和70×280的裂纹动态应力强度因子的相关系数为 0.9985.当t<0.5 ms时,裂纹尖端的应力强度因子几乎为0;当t≥0.5 ms时,裂纹尖端的应力强度因子随着时间的增加而逐渐增大,并呈现很小的震荡特性.变形后的简支梁如图11所示,裂纹基本沿着直线向上扩展.该简支梁变形后的应力分布如图12所示,裂纹尖端应力集中突出,水平方向应力值达2.09×10³ MPa.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同网格密度下K_I的历时曲线图

Fig.10 Time history of K_I at different mesh densities

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 变形后的简支梁(网格密度为50×200)

Fig.11 Deformed mesh for mesh density (at a mesh density of 50×200)

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 t=2 ms时刻的σ_x云图(网格密度为50×200)

Fig.12 Contour of σ_x at t=2 ms (at a mesh density of 50×200)

3 结语

标准有限元在处理时间积分时,在裂纹不断扩展的过程中整体刚度矩阵的自由度也会不断增大,从而导致迭代计算无法进行.本文提出的基于扩展有限单元法模拟动态裂纹扩展的方法提出了新的时间积分方案,将所有节点都富集Heaviside函数和裂纹尖端的渐近位移场函数,即每个节点都有12个自由度,从而使得总体刚度矩阵式保持一致,避免迭代计算式无法进行.并且提出了一种稀疏矩阵技术来解决矩阵所占内存大和计算时间长的问题.数值计算的结果表明,利用空间变换理论计算动力问题时,施加的荷载以膨胀波的形式传递,裂纹尖端的应力强度因子比荷载施加的时间稍有延迟,数值解的结果能够与解析的结果很好地吻合.线性荷载的数值结果比瞬时脉冲荷载的数值结果的震荡性更小,应力分布更加平稳光滑.不同网格密度条件下的数值计算结果相差不大,说明该方法计算裂纹扩展对网格的依赖性较小.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SHEN

J H

, WHEELER

, ILIC

, et al.

Application of open source FEM and DEM simulations for dynamic belt deflection modelling

[J]. Powder Technology, 2019, 357:171-185.

DOI:10.1016/j.powtec.2019.08.068 URL [本文引用: 1]

[2]

ELGUEDJ

, JAN

, COMBESCURE

, et al.

X-FEM Analysis of dynamic crack growth under transient loading in thick shells

[J]. International Journal of Impact Engineering, 2018, 122:228-250.

DOI:10.1016/j.ijimpeng.2018.08.013 URL [本文引用: 1]

[3]

SHARMA

, FUJISAWA

, MURAKAMI

Space-time FEM with block-iterative algorithm for nonlinear dynamic fracture analysis of concrete gravity dam

[J]. Soil Dynamics and Earthquake Engineering, 2020, 131:105995.

DOI:10.1016/j.soildyn.2019.105995 URL [本文引用: 1]

[4]

SUN

J S

, LEE

K H

, LEE

H P

Comparison of implicit and explicit finite element methods for dynamic problems

[J]. Journal of Materials Processing Technology, 2000, 105(1/2):110-118.

DOI:10.1016/S0924-0136(00)00580-X URL [本文引用: 1]

[5]

NILSSON

, LIDSTRÖM

Simulation of ductile fracture of slabs subjected to dynamic loading using cohesive elements

[J]. International Journal of Da-mage Mechanics, 2012, 21(6):871-892.

[本文引用: 1]

[6]

BELYTSCHKO

, BLACK

Elastic crack growth in finite elements with minimal remeshing

[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5):601-620.

DOI:10.1002/(ISSN)1097-0207 URL [本文引用: 1]

[7]

ZHOU

X P

, ZHANG

J Z

, BERTO

Fracture ana-lysis in brittle sandstone by digital imaging and AE techniques: Role of flaw length ratio

[J]. Journal of Materials in Civil Engineering, 2020, 32(5):04020085.

DOI:10.1061/(ASCE)MT.1943-5533.0003151 URL [本文引用: 1]

[8]

ZHOU

X P

, CHENG

Multidimensional space method for geometrically nonlinear problems under total Lagrangian formulation based on the extended finite-element method

[J]. Journal of Engineering Mechanics, 2017, 143(7):04017036.

DOI:10.1061/(ASCE)EM.1943-7889.0001241 URL [本文引用: 1]

[9]

CHEN

J W

, ZHOU

X P

The enhanced extended finite element method for the propagation of complex branched cracks

[J]. Engineering Analysis With Boundary Elements, 2019, 104:46-62.

DOI:10.1016/j.enganabound.2019.03.028 URL [本文引用: 1]

[10]

STOLARSKA

, CHOPP

D L

, MOËS

, et al.

Modelling crack growth by level sets in the extended finite element method

[J]. International Journal for Numerical Methods in Engineering, 2001, 51(8):943-960.

DOI:10.1002/nme.201 URL [本文引用: 2]

[11]

ZHOU

X P

, CHEN

J W

Extended finite element simulation of step-path brittle failure in rock slopes with non-persistent en-echelon joints

[J]. Engineering Geology, 2019, 250:65-88.

DOI:10.1016/j.enggeo.2019.01.012 URL [本文引用: 1]

[12]

CHEN

J W

, ZHOU

X P

, BERTO

The improvement of crack propagation modelling in triangular 2D structures using the extended finite element method

[J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(2):397-414.

[本文引用: 1]

[13]

黄宏伟, 刘德军, 薛亚东, 等.

基于扩展有限元的隧道衬砌裂缝开裂数值分析

[J]. 岩土工程学报, 2013, 35(2):266-275.

[本文引用: 1]

HUANG

Hongwei

, LIU

Dejun

, XUE

Yadong

, et al.

Numerical analysis of cracking of tunnel linings based on extended finite element

[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2):266-275.

[本文引用: 1]

[14]

阮滨, 陈国兴, 王志华.

基于扩展有限元法的均质土坝裂纹模拟

[J]. 岩土工程学报, 2013, 35(Sup.2):49-54.

[本文引用: 1]

RUAN

Bin

, CHEN

Guoxing

, WANG

Zhihua

Numerical simulation of cracks of homogeneous earth dams using an extended finite element method

[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Sup.2):49-54.

[本文引用: 1]

[15]

MENOUILLARD

, BELYTSCHKO

Dynamic fracture with meshfree enriched XFEM

[J]. Acta Mechanica, 2010, 213(1/2):53-69.

DOI:10.1007/s00707-009-0275-z URL [本文引用: 1]

[16]

WEN

L F

, TIAN

Improved XFEM: Accurate and robust dynamic crack growth simulation

[J]. Compu-ter Methods in Applied Mechanics and Engineering, 2016, 308:256-285.

[本文引用: 1]

[17]

ZHOU

X P

, ZHANG

J Z

, QIAN

Q H

, et al.

Expe-rimental investigation of progressive cracking processes in granite under uniaxial loading using digital imaging and AE techniques

[J]. Journal of Structural Geology, 2019, 126:129-145.

DOI:10.1016/j.jsg.2019.06.003 URL [本文引用: 1]

[18]

WANG

Y T

, ZHOU

X P

, XU

Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics

[J]. Engineering Fracture Mechanics, 2016, 163:248-273.

DOI:10.1016/j.engfracmech.2016.06.013 URL

[19]

Z J

, FAN

L F

, LIU

Q S

, et al.

Micro-mechanical modeling of the macro-mechanical response and fracture behavior of rock using the numerical manifold method

[J]. Engineering Geology, 2017, 225:49-60.

DOI:10.1016/j.enggeo.2016.08.018 URL [本文引用: 1]

[20]

CHEN

, HANSEN

J M

, TORTORELLI

D A

Unconditionally energy stable implicit time integration: Application to multibody system analysis and design

[J]. International Journal for Numerical Methods in Engineering, 2000, 48(6):791-822.

DOI:10.1002/(ISSN)1097-0207 URL [本文引用: 1]

[21]

WANG

J R

, WU

J C

, WANG

D D

A quasi-consis-tent integration method for efficient meshfree analysis of Helmholtz problems with plane wave basis functions

[J]. Engineering Analysis With Boundary Elements, 2020, 110:42-55.

DOI:10.1016/j.enganabound.2019.10.002 URL

[22]

WANG

D D

, WU

J C

An inherently consistent reproducing kernel gradient smoothing framework toward efficient Galerkin meshfree formulation with explicit quadrature

[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 349:628-672.

DOI:10.1016/j.cma.2019.02.029 URL [本文引用: 1]

[23]

WANG

D D

, WANG

J R

, WU

J C

, et al.

A three-dimensional two-level gradient smoothing meshfree method for rainfall induced landslide simulations

[J]. Frontiers of Structural and Civil Engineering, 2019, 13(2):337-352.

DOI:10.1007/s11709-018-0467-5 URL [本文引用: 1]

Application of open source FEM and DEM simulations for dynamic belt deflection modelling

2019

... 在工程建设和运营过程中,结构或者裂隙岩体会受到多种形式的动力作用(如爆破、地震等),在动荷载的作用下更容产生失稳破坏,故针对裂纹动态扩展的研究引起了广泛的关注^[1,2,3].Sun等^[4]基于有限元方法比较了显式时间积分和隐式时间积分在分析线性和非线性动力问题中的区别.2012年,Nilsson等^[5]在黏结单元中嵌入裂纹,分析了动荷载作用于弹塑性厚板的动力响应. ...

X-FEM Analysis of dynamic crack growth under transient loading in thick shells

2018

Space-time FEM with block-iterative algorithm for nonlinear dynamic fracture analysis of concrete gravity dam

2020

Comparison of implicit and explicit finite element methods for dynamic problems

2000

Simulation of ductile fracture of slabs subjected to dynamic loading using cohesive elements

2012

Elastic crack growth in finite elements with minimal remeshing

1999

... 扩展有限单元法(XFEM)^[6,7,8,9]是近十五年发展起来的一种在常规有限元框架内求解不连续问题,特别是裂纹扩展问题的数值方法.其原理是在裂纹影响区域的单元结点上用裂尖渐近位移场函数及跳跃函数加强传统有限元的基,以考虑由于裂纹存在引起的位移不连续性,继承了标准有限元的所有优点,但其所使用的网格与结构内部的几何和物理界面无关,从而避免了常规有限元方法中的网格重构,不需要裂纹面与有限元网格一致,不需要在裂缝周围布置高密度网格,大大简化了裂纹扩展的分析过程.能够很容易刻画出裂纹面上位移的强不连续性质和裂纹尖端的应力奇异性,并且无需重新划分网格.2001年,Stolarska等^[10]将水平集函数引入XFEM来描述裂纹的位置和裂纹扩展之后的更新位置.裂纹的几何位置能够很容易用两个零水平集函数来表达,这两个零水平集函数在裂纹尖端处彼此正交.同时,随着裂纹的扩展,裂纹面和裂纹尖端处需要富集的节点能够实时更新. ...

Fracture ana-lysis in brittle sandstone by digital imaging and AE techniques: Role of flaw length ratio

2020

Multidimensional space method for geometrically nonlinear problems under total Lagrangian formulation based on the extended finite-element method

2017

The enhanced extended finite element method for the propagation of complex branched cracks

2019

Modelling crack growth by level sets in the extended finite element method

2001

... Stolarska等^[10]给出了水平集法的更新算法,水平集函数

ϕ (x)

的更新算法为 ...

Extended finite element simulation of step-path brittle failure in rock slopes with non-persistent en-echelon joints

2019

... Zhou等^[11]在推导扩展有限元算法的基础上,分析了应力强度因子的J积分计算方法及积分区域的选取.基于扩展有限元法对I型裂纹进行了计算,有限元网格独立于裂纹面,无需在裂纹尖端加密网格.Chen等^[12]引入裂纹交叉汇合加强函数以分析多裂纹交叉汇合过程,并且在裂纹附近区域使用广义形函数,并引入线增函数消除混合单元,可有效提高裂纹附近的精度.黄宏伟等^[13]在这些研究的基础上,采用扩展有限元研究了衬砌在主要影响因素作用下的裂缝分布规律、裂缝扩展过程、裂缝外观表现形式及发生机制.阮滨等^[14]基于扩展有限元法对均质土坝坝顶的初始裂纹扩展路径进行了模拟,研究结果表明扩展有限元法对网格划分的要求比较高,网格须均匀,网格的疏密程度对计算的结果影响不大.Menouillard等^[15]提出利用无网格近似方法的XFEM富集方案,该方法采用显式时间积分方案来分析动力过程.Wen等^[16]基于改进的扩展有限单元法研究了裂纹动态扩展问题的计算精度和算法稳定性问题. ...

The improvement of crack propagation modelling in triangular 2D structures using the extended finite element method

2019

基于扩展有限元的隧道衬砌裂缝开裂数值分析

2013

基于扩展有限元的隧道衬砌裂缝开裂数值分析

2013

基于扩展有限元法的均质土坝裂纹模拟

2013

基于扩展有限元法的均质土坝裂纹模拟

2013

Dynamic fracture with meshfree enriched XFEM

2010

Improved XFEM: Accurate and robust dynamic crack growth simulation

2016

Expe-rimental investigation of progressive cracking processes in granite under uniaxial loading using digital imaging and AE techniques

2019

... 水平集法是裂纹和非连续面追踪强有力的工具.Zhou等^[17]首次引入水平集法来研究材料内部界面的追踪定位和形状描述.如图2所示,一根裂纹可以用2个在裂纹尖端彼此相互正交的零水平集函数

ϕ (x)

和

ψ (x)

表示. ...

Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics

2016

Micro-mechanical modeling of the macro-mechanical response and fracture behavior of rock using the numerical manifold method

2017

... 根据Wu等^[19]的研究,线弹性材料中的I型、II 型及 III 型裂纹尖端渐近位移场均可由几个特定的基函数组成的函数形式来表达,为了能体现出裂纹尖端渐近位移场的奇异性,将该组基函数引入裂纹尖端的位移场计算,如下: ...

Unconditionally energy stable implicit time integration: Application to multibody system analysis and design

2000

... 根据Newmark时间积分方法,式(39)求解稳定的条件是ξ和η应满足^[20]: ...

A quasi-consis-tent integration method for efficient meshfree analysis of Helmholtz problems with plane wave basis functions

2020

An inherently consistent reproducing kernel gradient smoothing framework toward efficient Galerkin meshfree formulation with explicit quadrature

2019

... 根据Wang等^[22,23]的研究,裂纹尖端的应力强度因子K_I的解析解为 ...

A three-dimensional two-level gradient smoothing meshfree method for rainfall induced landslide simulations

2019

... 根据Wang等^[22,23]的研究,裂纹尖端的应力强度因子K_I的解析解为 ...

〈

〉